Circuit Simulates One-Dimensional Quantum System

Emanuele Dalla Torre; Eran Sela

Viewpoint

Circuit Simulates One-Dimensional Quantum System

Emanuele Dalla Torre

Department of Physics and Center for Quantum Entanglement Science and Technology, Bar-Ilan University, Ramat Gan, Israel

Eran Sela

School of Physics and Astronomy, Tel Aviv University, Tel Aviv, Israel

September 19, 2018• Physics 11, 94

An electrical circuit simulates a quantum phase transition induced by the presence of an impurity in a one-dimensional conductor.

Figure caption — **Figure 1:** Three physical systems can exhibit the same insulator-to-metal quantum phase transition thought to occur in a 1D system of quantum particles, known as a Tomonaga-Luttinger liquid (TLL). The systems are: Two superconductors separated by a thin resistive layer (top left) [2]; a 1D array of electrons in the presence of an impurity (top right) [6]; and a micrometer-sized electronic device made of nanochannels connected to a central quantum dot (bottom) [1]. Pierre and colleagues have used the latter as a quantum simulator, which allows them to investigate features of the TLL phase transition that can’t be studied in the other two systems.

According to the laws of classical physics, atoms should stand perfectly still at absolute zero. However, this classical prediction violates the Heisenberg uncertainty principle, which says particles always fluctuate, even at zero temperature. Such fluctuations can drive a transition between two quantum phases at zero temperature, much like thermal fluctuations drive a phase transition at finite temperatures. While quantum phase transitions have been observed in a handful of condensed-matter systems, it remains challenging to test them in experiments. Frédéric Pierre at the University of Paris Sud and collaborators have now demonstrated an electronic circuit that can simulate a quantum phase transition that is expected to occur in a one-dimensional (1D) quantum liquid, such as electrons in a long, thin wire [1]. In such a liquid, the presence of an impurity can trigger the transition of the otherwise conducting wire to an insulating state. By simulating this insulator-to-metal transition, with unprecedented control over the parameters governing the transition, the team was able to test previously inaccessible aspects of a fundamental theory for 1D quantum systems. The approach may pave the way to simulating other quantum phase transitions using electronic devices.

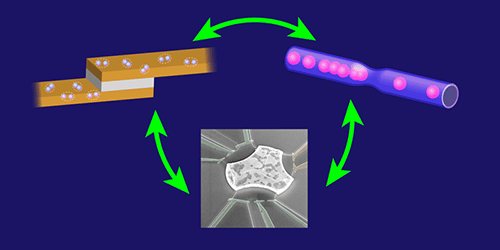
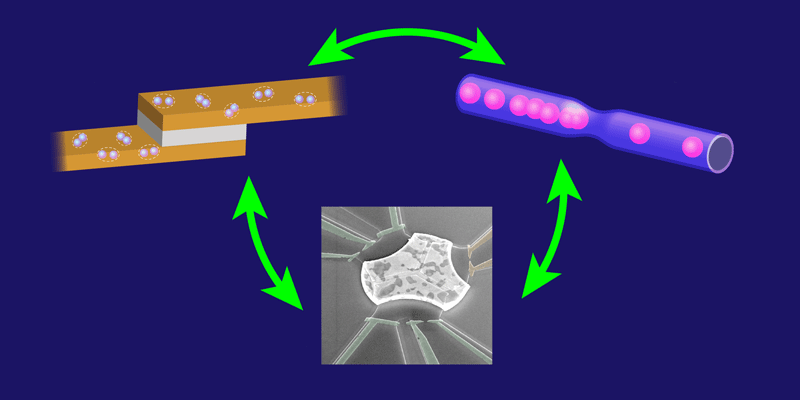
The quantum phase transition observed by Pierre and collaborators traces back to a 1982 theoretical prediction by physicists Sudip Chakravarty [2] and Albert Schmid [3], who studied a structure made of a metal sandwiched between two superconductors, known as a resistively shunted Josephson junction [Fig. 1(top left)]. Does this device behave as a superconductor or as a metal? Chakravarty and Schmid solved this problem by recasting it in terms of a known problem of statistical mechanics: the behavior of a gas of charged particles in one dimension, or a “Coulomb gas” [4].

Chakravarty and Schmid found that the behavior of the junction depends only on the physical properties of the metal, specifically on its resistance. In quantum mechanics, the resistance is often measured in terms of a resistance quantum, defined as $h ∕ {(2 e)}^{2}$ , or $6.5 k Ω$ , where $e$ is the charge of an electron and $h$ is Plank’s constant. Their calculations showed that if the resistance of the metal is larger than $6.5 k Ω$ , the junction behaves as a regular metal, but if it is smaller, the junction behaves as a superconductor. Their theory predicted that a quantum phase transition between these two states occurs exactly at $6.5 k Ω$ . The resistance value controls the phase transition because resistors have two effects: they dissipate the electrons’ energy, and in doing so, they add quantum fluctuations to the system. According to statistical mechanics, these two effects are connected by the fluctuation-dissipation relation, and they exactly balance each other. Hence, by controlling the resistance of the metal, one can “tame” quantum fluctuations and thereby control the quantum phase transition between the metallic and superconducting states [5].

Chakravarty and Schmid’s results can be extended to a broader class of physical systems. In 1992, Charles Kane and Matthew Fisher used the same equations to describe a quantum impurity embedded in a 1D wire of particles [Fig. 1(top right)] [6]. Such a 1D system, in which particles cannot avoid each other, is often described as a Tomonaga-Luttinger liquid (TLL)—a unique phase of matter that is thought to describe, for instance, electrons in carbon nanotubes or electrons moving along the edges of a quantum Hall material. Other 1D systems, such as a spin chain with a weak link [7], were found to be described by the same equations.

Kane and Fisher predicted the possibility of a quantum phase transition between a metallic state, unaffected by the impurity, and an insulating state in which the impurity splits the wire into two disconnected parts. The phase transition is controlled by the so-called Luttinger interaction parameter $K$ , which quantifies the strength of the interaction between the particles in the wire and effectively controls the fate of the system when the impurity is introduced. Up to now, however, these theoretical predictions could not be tested in experiments. The key challenge is posed by the fact that the value of $K$ is hard to control experimentally.

Pierre and colleagues have devised a platform in which the same type of quantum phase transition can be experimentally observed [Fig. 1(bottom)]. Their system is a micrometer-sized device made of a series of 1D channels in which electrons can move only in one direction. To create these channels, the researchers use the edge states of a semiconductor heterostructure in a quantum Hall regime. The channels are connected to a central microscopic island—a quantum dot—that can be occupied by a known number of electrons. The junctions between each of the channels and the island act as “quantum point contacts”—narrow constrictions whose sizes are comparable to the wavelength of the conducting electrons. The researchers can then control the number of channels coupled to the quantum dot by opening or closing these quantum point contacts through an applied voltage.

As shown by a previous theoretical study [8], the authors’ device is equivalent to an infinitely long 1D wire of electrons interacting with an impurity. The island blocks the transmission of electrons from one channel to other channels, mimicking an impurity that blocks the flow of electrons in a 1D wire. The team varied the Luttinger interaction strength $K$ by controlling the number of open channels coupled to the dot. By coupling one, two, three, or four channels to the dot, they could tune $K$ to four different values (1/2, 2/3, 3/4, and 4/5). This unprecedented tunability is what distinguishes this experiment from previous studies that employed similar circuit analogs but couldn’t tune the value of $K$ [9].

Using this setup, the team carried out experiments that confirmed previous predictions for a specific value of the interaction strength, $K = 1 ∕ 2$ [10], and also confirmed calculations performed within the present paper for an additional value of $K = 2 ∕ 3$ . For such values, the experiments showed evidence of an insulator-to-metal phase transition. The features of this transition, such as the scaling behavior of the device conductance as a function of temperature, accurately reproduced the theoretical expectations. Importantly, good agreement between theory and experiment was also found for out-of-equilibrium conditions, in which the system was perturbed by a large voltage applied to the island. Nonequilibrium states are generally harder and, in some cases, impossible to analyze theoretically. Remarkably, the experiments could also access regimes for which no explicit theoretical solutions are yet available: interaction strengths of $K = 3 ∕ 4$ and $4 ∕ 5$ , both for equilibrium and out-of-equilibrium conditions.

The scheme developed by Pierre and his collaborators can be regarded as a quantum simulator [11]. The idea—envisioned by Feynman nearly four decades ago—is to use a measurable quantum system to mimic another quantum system that is governed by the same equations but is theoretically intractable. Thanks to the mathematical equivalence between Josephson junctions, Tomonaga-Luttinger liquids, and this quantum-dot circuit, each of these systems can be used as a quantum simulator of the other two (Fig. 1). As the experiments of Pierre and co-workers demonstrate, this approach can help us solve quantum problems that no theory or supercomputer could settle.

This research is published in Physical Review X.

References

A. Anthore, Z. Iftikhar, E. Boulat, F. D. Parmentier, A. Cavanna, A. Ouerghi, U. Gennser, and F. Pierre, “Circuit quantum simulation of a Tomonaga-Luttinger liquid with an impurity,” Phys. Rev. X 8, 031075 (2018).
S. Chakravarty, “Quantum fluctuations in the tunneling between superconductors,” Phys. Rev. Lett. 49, 681 (1982).
A. Schmid, “Diffusion and localization in a dissipative quantum system,” Phys. Rev. Lett. 51, 1506 (1983).
Interestingly, their derivation is mathematically equivalent to the identification of topological charges in two-dimensional superconductors found by Kosterliz and Thouless, for which they were awarded the Noble prize in Physics in 2016; J. M. Kosterlitz and D. J. Thouless, “Ordering, metastability and phase transitions in two-dimensional systems,” J. Phys. C 6, 1181 (1973); The Kosterlitz-Thouless transition can be described using a sine-Gordon quantum field theory, while the Chakravarty-Schmid model corresponds to the boundary sine-Gordon problem.
R. P. Feynman and F. L. Vernon, “The Theory of a general quantum system interacting with a linear dissipative system,” Ann. Phys. 24, 118 (1963); A. O. Caldeira and A. J. Leggett, “Quantum tunnelling in a dissipative system,” Ann. Phys. 149, 374 (1983).
C. L. Kane and M. P. A. Fisher, “Transport in a one-channel Luttinger liquid,” Phys. Rev. Lett. 68, 1220 (1992).
S. Eggert and I. Affleck, “Magnetic impurities in half-integer-spin Heisenberg antiferromagnetic chains,” Phys. Rev. B 46, 10866 (1992).
I. Safi and H. Saleur, “One-channel conductor in an ohmic environment: Mapping to a Tomonaga-Luttinger liquid and full counting statistics,” Phys. Rev. Lett. 93, 126602 (2004).
H. T. Mebrahtu, I. V. Borzenets, D. E. Liu, H. Zheng, Y. V. Bomze, A. I. Smirnov, H. U. Baranger, and G. Finkelstein,, “Quantum phase transition in a resonant level coupled to interacting leads,” Nature 488, 61 (2012).
P. Fendley, A. Ludwig, and H. Saleur, “Exact conductance through point contacts in the $𝜈 = 1 ∕ 3$ fractional quantum Hall effect,” Phys. Rev. Lett. 74, 3005 (1995).
R. Feynman, “Simulating physics with computers,” Int. J. Theor. Phys. 21, 467 (1982).

About the Authors

Emanuele G. Dalla Torre is a senior lecturer in the Department of Physics of Bar-Ilan University, Israel. Born in Italy, he earned his academic degrees in Israel, first at the Technion – Israel Institute of Technology and then at the Weizmann Institute of Science. After his Ph.D., in 2011, he moved to Harvard University for three years of postdoctoral training. His research concerns theoretical aspects of the dynamics of large quantum systems. He is fascinated by the idea that complex, nonequilibrium, many-body quantum problems can often be described in terms of a small set of classical equations of motion.

Eran Sela is an associate professor at Tel Aviv University. He earned a B.Sc. in physics and mathematics at Bar-Ilan University and a Ph.D. in physics at the Weizmann Institute of Science. Prior to joining Tel Aviv University, he worked as a research fellow at the University of British Columbia (2007–2009) and at the University of Cologne (2009–2012). His research interests include the analysis of strongly correlated electronic systems, low-dimensional systems (quantum wires, quantum dots), topological phases of matter, and quantum entanglement in many-body systems.