A New Model for Electrolyte Conductivity
A battery’s performance depends on how well its ions transport electrical charges. To boost the conductivity, one can increase the concentration of ions in the electrolyte. But if the concentration gets too high, the ions aggregate in clusters, which reduces the conductivity. Now, Arthur France-Lanord and Jeffrey Grossman at the Massachusetts Institute of Technology, Cambridge, have developed a model for calculating the ionic conductivity of concentrated electrolytes in the presence of such clusters. Their method provides insights into the physical mechanisms of ion conduction and could help researchers more efficiently screen for new battery electrolytes.
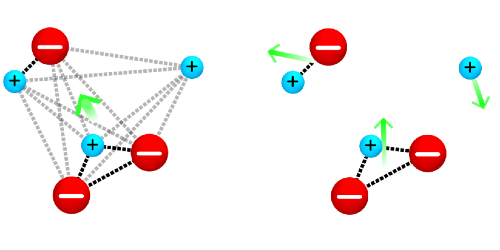
Calculations of ionic conductivity often rely on the Nernst-Einstein equation, which assumes that the ions are noninteracting particles that contribute to the conductivity via their charge and ability to diffuse. In concentrated electrolytes where ions strongly interact, this assumption breaks down. Compared with idealized, noninteracting ions, ion clusters form with a reduced net charge and an altered diffusivity, so calculations of conductivity are off by orders of magnitude.
Instead of accounting for all possible interactions, which would be computationally costly, France-Lanord and Grossman developed a Nernst-Einstein formalism for the clusters. Their model allows for all possible types of clusters but makes the assumption that clusters, once formed, do not interact with one another. The duo applied their approach to an ideal electrolyte model with a known cluster population. These results agreed with a more time-consuming exact calculation. Then they calculated the conductivity of lithium ions in a standard polymer electrolyte, which showed that their model could explain recent peculiar experimental results in terms of cations trapped in negatively charged clusters.
This research is published in Physical Review Letters.
–Nicolas Doiron-Leyraud
Nicolas Doiron-Leyraud is a Corresponding Editor for Physics based in Montreal, Canada.