A Speed Test for Ripples in a Quantum System

Marc Cheneau; Laurent Sanchez-Palencia

Viewpoint

A Speed Test for Ripples in a Quantum System

Marc Cheneau¹ and Laurent Sanchez-Palencia²

¹Laboratoire Charles Fabry, Institut d’Optique, CNRS, Université Paris Saclay, Palaiseau, France
²Center for Theoretical Physics, Institut Polytechnique de Paris, Palaiseau, France

July 13, 2020• Physics 13, 109

Settling a theoretical debate, three studies show that there is a maximum speed at which a physical effect can travel through systems of long-range-interacting particles.

Figure caption — **Figure 1:** A flipped spin in a chain of interacting spins (bottom) will eventually stir its neighbors (middle and top). New studies of spin systems [2–4] show that, for long-range interactions decaying sufficiently fast, the speed of this physical effect has a fixed upper limit—meaning it lies in an effective light cone in space and time (solid line). For longer ranged interactions, however, this light cone could, in principle, be flared (with a changing speed bound, as shown with the dotted line). Or, it might not exist at all.

Are there limits on how fast a physical effect can propagate in a system? The answer to this fundamental question has far-reaching consequences for practically any dynamic system we want to use or understand, from media for sending long-distance messages to extended bodies approaching thermal equilibrium. In a pioneering 1972 study, Elliott Lieb and Derek Robinson showed that the speed at which a physical effect could travel through a collection of interacting particles always has an upper limit [1]. The existence of the Lieb-Robinson bound, however, assumes that the particles are locally interacting, whereas many forms of “complex matter” of interest today involve long-range interactions. In a trio of papers, researchers now establish a bound for many long-range systems as well [2–4]. The findings settle a recent debate over if and when such bounds exist, and they may have implications for the choice of platform for quantum computation and other quantum technologies.

You may have raised an eyebrow upon reading that the Lieb-Robinson bound was considered a discovery. After all, special relativity says that the speed of light is the ultimate limit on how fast a signal can travel, and this limit is built into the quantum field theory that describes the interactions between elementary particles. But researchers are also interested in whether an intrinsic limit on the speed of a physical effect exists simply by virtue of the way a system’s particles interact. This limit determines, for instance, how quickly a jolt to an atom in a solid will influence a distant atom’s behavior.

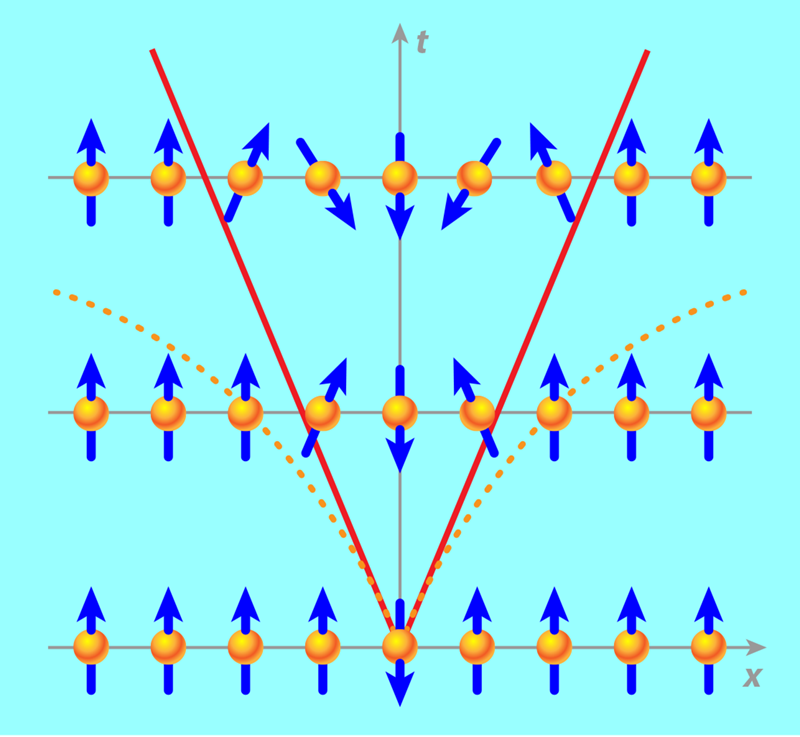
When Lieb and Robinson explored this bound, they used a lattice of spins as a generic model of matter on a microscopic scale, where quantum mechanics prevails. The interactions in their model refer, for instance, to the energy cost of two spins pointing in opposite directions. The interactions are also short-ranged because the energy cost falls off exponentially with the distance between two spins, as $exp (- x ∕ d) .$ Lieb and Robinson defined their “physical effect” as a correlation between two distant spins. Consider, for instance, a lattice with all spins initially aligned upwards (Fig. 1). Now imagine flipping one spin at $x = 0$ . It will mainly stir its closest neighbors, which will stir theirs, and so on, and it will take some time $t$ before a spin at a distant point $x$ feels the initial flip. Lieb and Robinson quantified this correlation onset between distant spins with a so-called commutator, a mathematical object involving the quantum spin operator acting at $x = 0$ and $t = 0$ and the quantum spin operator acting at $x$ and $t$ . They showed that there is always a velocity $v$ such that the “norm” of this commutator is negligibly small when $x > v t$ . In modern language, physicists would say the speed of a physical effect is bound to an effective light cone (Fig. 1)—akin to the causal light cone of relativity. The slope of this cone is $v$ , and the fact that it’s constant means that the bound doesn’t speed up or slow down with time.

Compared to the spin system Lieb and Robinson studied, many quantum systems of interest today involve longer-ranged interactions, such as arrays of Rydberg atoms, trapped ions and molecules, and defects in solids. The availability of such systems has stimulated researchers to extend Lieb and Robinson’s work to systems with power-law interactions, decaying as $1 ∕ x^{𝛼}$ . Various studies found bounds that, in principle, allow the propagation of a physical effect at a velocity that increases over time—implying a “flared” light cone [5–7]. But other analyses, relying on numerical calculations or analytical calculations with simplified models, suggested that a linear light cone would exist provided that $𝛼$ is sufficiently large [6, 8, 9]. With mathematical proofs, the three new studies look at a variety of long-range-interacting systems and determine that there is a critical value of $𝛼$ that separates bounded and unbounded dynamics. And they find this critical value as well.

The first study was reported in a 2019 paper by Chi-Fang Chen and Andrew Lucas, then both at Stanford University. The two considered a generic 1D spin system with power-law interactions. And they determined a bound to the usual commutator norm by calculating the magnitude of its largest eigenvalue. For $𝛼 > 3$ , they found that the time for a signal to reach a certain distance is at least proportional to the distance, hence establishing a light cone with straight sides.

A more recent paper from Tomotaka Kuwahara of the RIKEN Center for Advanced Intelligence Project and Keiji Saito of Keio University, both in Japan, generalizes Chen and Lucas’ theorem by extending it to dimension $D > 1$ . They find a straight cone for $𝛼 > 2 D + 1$ . Moreover, they show that $2 D + 1$ is a tight threshold by demonstrating a scenario that violates the light cone for $𝛼 < 2 D + 1 .$

Finally, the third paper, from Minh Tran of the Joint Quantum Institute in Maryland, in collaboration with Lucas, Chen, and other researchers, uses different definitions of the norm to establish a new hierarchy of light cones. The most generally defined norm holds in any system and for any signal when $𝛼 > 2 D + 1$ . But in some specific cases a light cone exists as soon as $𝛼 > 3 D ∕ 2 + 1$ or even $𝛼 > D + 1$ for noninteracting particles. The existence of these tighter bounds sheds light on experimental and numerical observations where the propagation of a signal in a system seemed to be bounded by a light cone even when the particle interactions decayed slowly.

The three studies leave us with the picture that, as long as interactions decay fast enough, the speed of physical effects has an upper bound. This result is disappointing to anyone who dreams of using quantum mechanics to speed up the communication between two parts. But the limit could be an advantage. It means, for example, that a quantum memory should be safe from the perturbations of the outside world for a certain period of time. It also says that simulating some quantum systems on a classical computer might be doable because one doesn’t have to account for the influence of every distant particle. At the same time, the new studies help us better understand the properties of complex quantum matter and the systems experimentalists use to simulate them [10, 11].

Finally, we should remember that these works say how fast information can propagate, not how fast it does propagate. To answer this more practical question, one needs to know the microscopic mechanism driving the propagation, which involves the system’s elementary excitations [12].

This research is published in Physical Review Letters and Physical Review X.

References

E. H. Lieb and D. W. Robinson, “The finite group velocity of quantum spin systems,” Commun. Math. Phys. 28, 251 (1972).
C. F. Chen and A. Lucas, “Finite speed of quantum scrambling with long range interactions,” Phys. Rev. Lett. 123, 250605 (2019).
M. C. Tran et al., “Hierarchy of linear light cones with long-range interactions,” Phys. Rev. X 10, 031009 (2020).
T. Kuwahara and K. Saito, “Strictly linear light cones in long-range interacting systems of arbitrary di-mensions,” Phys. Rev. X 10, 031010 (2020).
M. B. Hastings, “Locality in quantum systems,” in Quantum Theory from Small to Large Scales: Lecture Notes of the Les Houches Summer School, Volume 95, August 2010, edited by J. Frohlich et al. (Oxford University Press, Oxford, 2012), p. 171[Amazon][WorldCat].
J. Eisert et al., “Breakdown of quasilocality in long-range quantum lattice models,” Phys. Rev. Lett. 111, 260401 (2013).
M. Foss-Feig et al., “Nearly linear light cones in long-range interacting quantum systems,” Phys. Rev. Lett. 114, 157201 (2015).
P. Hauke and L. Tagliacozzo, “Spread of correlations in long-range interacting quantum systems,” Phys. Rev. Lett. 111, 207202 (2013).
L. Cevolani et al., “Protected quasilocality in quantum systems with long-range interactions,” Phys. Rev. A 92, 041603 (2015).
P. Jurcevic et al., “Quasiparticle engineering and entanglement propagation in a quantum many-body system,” Nature 511, 202 (2014).
P. Richerme et al., “Non-local propagation of correlations in quantum systems with long-range interactions,” Nature 511, 198 (2014).
P. Calabrese and J. Cardy, “Time dependence of correlation functions following a quantum quench,” Phys. Rev. Lett. 96, 136801 (2006).

About the Authors

Marc Cheneau is a CNRS researcher at the Institute of Optics in France and an experimentalist in the field of quantum gases. He earned his Ph.D. in 2009 from École Normale Supérieure in Paris, where he studied the bidimensional superfluid transition in Bose gases. He then joined the Max Planck Institute for Quantum Optics in Germany, where he participated in the pioneering development of a quantum gas microscope and observed for the first time the ballistic propagation of correlations in quantum gases. His current research focuses on the relaxation dynamics of quantum gases.

Laurent Sanchez-Palencia is a senior CNRS researcher and an associate professor at the École Polytechnique in France. He earned a Ph.D. in physics at École Normale Supérieure in Paris in 2003. He then was a Humboldt postdoctoral fellow at the Institute for Theoretical Physics in Germany. He created the quantum matter group at the Institute of Optics, France, and then moved his group to the Institut Polytechnique de Paris in 2016. His research interests include the theory of disordered systems, many-body quantum systems, quantum simulations, and ultracold atoms. He is the recipient of the Leconte prize of the French Academy of Sciences and of a European Research Council (ERC) grant.