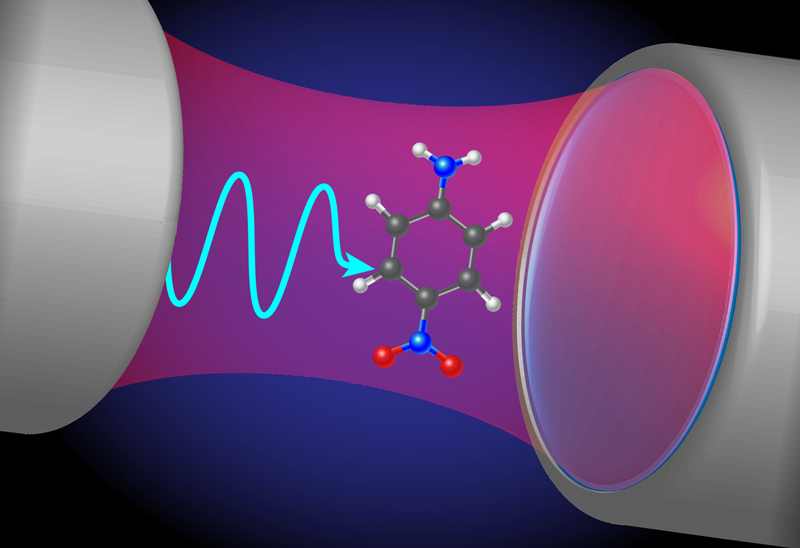
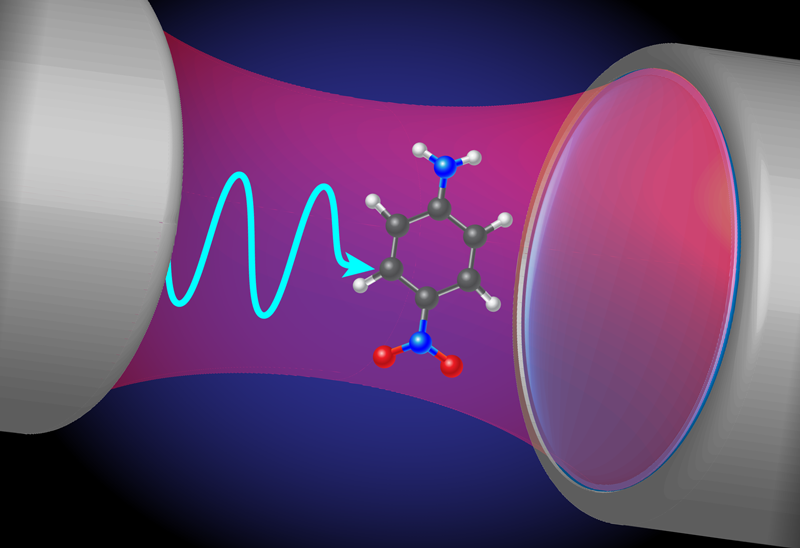
A Comprehensive Framework for Modeling Molecular Polaritons
Phenomena founded on the quantum nature of light have traditionally been the focus of quantum optics. In the past few years, researchers in other fields have gotten in on the act, leveraging light’s quantum properties to drive transformations in materials and molecules [1]. One recent development in this vein—made possible by new ways of achieving the strong coupling of light with few-atom systems—is the creation of novel states with characteristics of both light and matter. In this regime of strong coupling, light and matter meet on the same quantized footing and form quasiparticles called polaritons. Creating and controlling such coupling between light and molecules could allow the manipulation of a molecule’s electronic structure in a way that opens new avenues for quantum chemistry, but the theoretical description required to realize this potential has been lacking. Now, Tor Haugland, at the Norwegian University of Science and Technology, and colleagues have developed the necessary framework with a computational approach that accurately predicts how molecules interact with quantized electromagnetic fields [2].
When a molecule is placed into an optical cavity, the molecule’s quantum states naturally interact and hybridize with the quantum states of the cavity’s electromagnetic field. Such light-matter coupling can result in changes to the molecule’s ground-state potential-energy surface (PES), modifying the ground-state reactivity of the molecule. The excited-state properties of the molecule-cavity system are modified by strong coupling even more dramatically. The newly formed light-matter polaritonic states can completely change the landscape of the original molecular PES, altering the pathways of the molecule’s excited-state chemical reactions.
Modifying chemical reactions in this way has been shown to be possible by strong-coupling chemistry experiments [3]. But a theoretical picture that captures all of the ingredients in these reactions has remained elusive. In this regime of correlated light-matter interactions, the well-established theory concepts of quantum chemistry, nanophotonics, and quantum optics are no longer individually sufficient. Traditional methods from quantum chemistry, such as the Born–Oppenheimer approximation, Hartree–Fock theory, coupled-cluster theory, or density-functional theory, describe the quantum-mechanical nature of the states in matter, but they do not account for the quantized electromagnetic field. On the other hand, methods from quantum optics typically explore the quantum electromagnetic field in considerable detail but describe the molecule via simplified models. Both over-simplifications are far from a realistic ab initio description of the relevant chemical dynamics, where many atoms and molecules (each with electronic and nuclear degrees of freedom) are coupled strongly to the vacuum electromagnetic field.
Theoretical tools exist to describe the strong coupling of light with matter. Perhaps the most amenable is the one known as quantum electrodynamical density-functional theory (QEDFT), which reformulates the Schrödinger equation to treat photons and electrons at the same level of quantization. But while this tool can handle a number of cases that involve electrons interacting with light [4, 5], it is limited to scenarios where the electrons and light can be treated as independent (uncorrelated) particles.
In this context, the work by Haugland and colleagues presents an important theoretical generalization of ab initio coupled-cluster theory to incorporate quantum electrodynamics. Coupled-cluster theory is a well-established technique for applying principles of quantum physics to predict chemical interactions. In the new generalized version, strong correlation effects between electrons and photons are incorporated systematically and consistently; that is, including correlation effects in the ground state. Using this method, the researchers show that quantum fields can manipulate charge-transfer excitations and the photochemistry of molecules. Their work confirms that an optical cavity can change the ground- and excited-state properties of molecules as well as the interactions between those states.
With this full quantum description of light and matter, researchers could unravel quantum effects in chemistry and catalysis, leading to dramatic improvements in various molecular properties of technological interest. For example, it offers a way to direct reactions involving molecules in an optical cavity. The properties of these molecules are dictated by their interaction with the cavity light, and they can be used as catalysts and sensors in the technologically important infrared-terahertz band.
Another interesting case is when an optical mode strongly couples with an infrared-active molecular vibration. This coupling should induce dramatic changes to the interactions among the molecule’s internal vibrations and, in turn, the dynamics of the molecule’s nuclei. The new framework from Haugland and colleagues will allow an accurate study of both the interactions and the nuclear dynamics. These interactions play a fundamental role in chemical reactivity and dynamics—for example, in shuttling energy among optically excited states in photosynthesis and in driving conformational changes in proteins [6, 7].
So far, the new framework—like most theoretical approaches that describe the strong coupling of light with a molecule—assumes perfect cavities whose modes are decoupled from any reservoirs; that is, the modes don’t lose energy or dephase. In reality, experiments are frequently performed with moderately to highly lossy cavities. To reach the light-matter strong coupling regime in such a lossy situation, the characteristic timescale of the coupling must be faster than the intrinsic losses of the excitations of the cavity or the molecule. If the losses prevail, the system is in the weak-coupling regime, in which the light-matter interaction shortens the molecules’ excited-state lifetime but does not lead to the formation of polariton states. For this reason, generalizing Haugland and co-workers’ framework to cover the regime of lossy cavities would be an important next step.
References
- J. Flick et al., “Strong light-matter coupling in quantum chemistry and quantum photonics,” Nanophoton. 7, 1479 (2018).
- T. S. Haugland et al., “Coupled cluster theory for molecular polaritons: Changing ground and excited states,” Phys. Rev. X 10, 041043 (2020).
- A. Thomas et al., “Tilting a ground-state reactivity landscape by vibrational strong coupling,” Science 363, 615 (2019).
- J. Flick et al., “Atoms and molecules in cavities, from weak to strong coupling in quantum-electrodynamics (QED) chemistry,” Proc. Natl. Acad. Sci. U.S.A. 114, 3026 (2017).
- J. Flick and P. Narang, “Cavity-correlated electron-nuclear dynamics from first principles,” Phys. Rev. Lett. 121, 113002 (2018).
- J. A. Campos-Gonzalez-Angulo et al., “Resonant catalysis of thermally activated chemical reactions with vibrational polaritons,” Nat. Commun. 10, 4685 (2019).
- A. H. Proppe et al., “Bioinspiration in light harvesting and catalysis,” Nat. Rev. Mater. 5, 828 (2020).