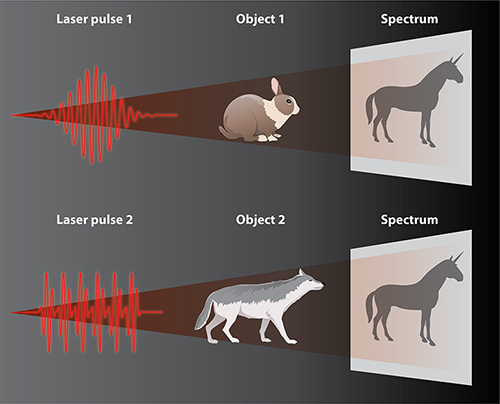
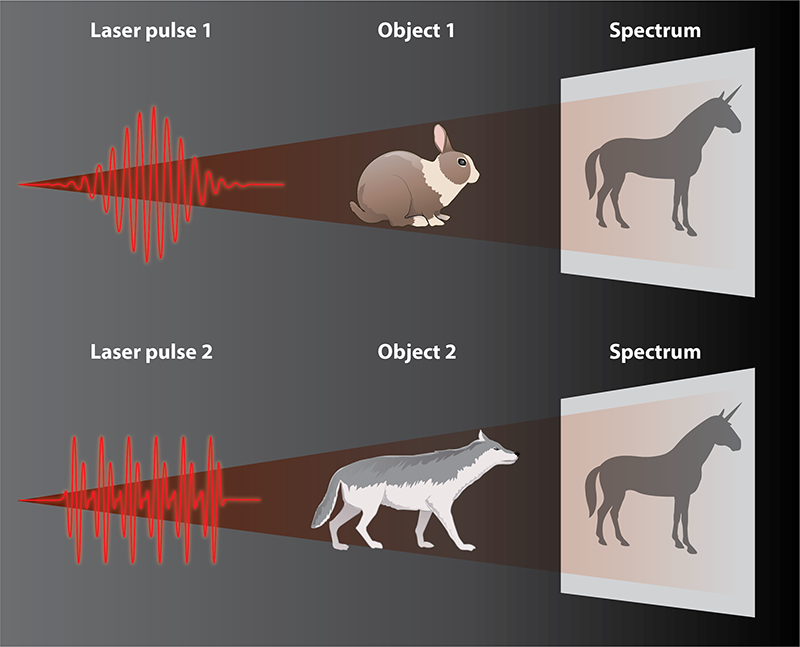
Making Materials Mimic Each Other
The puzzle of whether one can “hear the shape of a drum” [1] can be traced back to Hermann Weyl. The original question asks whether knowledge of the spectrum of a physical system uniquely determines its structure. An interesting twist on this question is whether one could make two time-dependent systems have the same properties by applying external “control fields” that also change with time. Now, Gerard McCaul, of Tulane University in Louisiana, and colleagues have proposed a new way to make one material behave like another by applying specially designed time-dependent fields such as laser pulses [2, 3]. The technique may let researchers manipulate the properties of different materials and study exotic materials that are otherwise hard to create.
Controlling how a quantum-mechanical system responds to time-dependent external fields, a technique called coherent control, is central to many areas of science and technology. For example, coherent control is used regularly in nuclear magnetic resonance experiments to prepare desired quantum states of qubits with radio-frequency pulses. Finding the ultimate limits to which tailoring the coherent control field can alter observables of a quantum system is therefore of great interest.
A natural question that follows is whether two distinct quantum systems can be made to have the same observable properties through coherent control. For example, can two atomic species, under the action of two different strong driving fields, be made to have the exact same spectrum of emitted light? This idea of spectral mimicry is appealing because it could potentially allow researchers to use readily available and well-understood materials to replicate the properties of exotic materials and thus reproduce phenomena that are usually hard to observe. Hopes in this direction include, for example, inducing superconductivity in new materials that usually do not have this property and creating photonic insulators—materials that block the transmission of light in one direction or another.
In 2017, researchers confirmed spectral mimicry to be theoretically possible by showing that two distinct atoms could have the same light emission spectrum under the proper choices of external, time-dependent electromagnetic fields [4]. This work had direct implications in the field of high harmonic generation (HHG), a highly nonlinear phenomenon in which a system driven by a strong electromagnetic field emits light with frequencies several times that of the driving field [5]. In this earlier work, each atom was described using a single-electron model. The puzzle intensifies in systems of many interacting electrons, such as solids. If coherent control can indeed be used to alter the system’s response, does it mean that insulators can be made to mimic conductors by application of the right control field?
McCaul et al. address this specific question, using it as an example of the principle that one many-electron system can act like another. They focus on the 1D Fermi-Hubbard model—a simplified model that describes a solid as a system of interacting fermions confined to sites on a lattice. The model has a (Mott) insulating phase and a conducting phase. Which phase the system is in depends on the ratio of its kinetic energy to its potential energy; the kinetic energy is associated with the electrons moving to different lattice sites, and the potential energy is associated with interactions between electrons. Typically, these two phases display different currents when exposed to external laser fields. And since the electric currents determine the emission of the system, the two phases would produce different spectra as well. But McCaul et al. found a way to apply suitable laser fields that would make the emission spectra of both phases identical, so that one system can “mimic” the behavior of another. Put another way, one can make two differently shaped drums sound identical under certain conditions.
This newly proposed mimicry scheme is based on an existing idea related to coherent control called tracking control [6]—a formula of sorts for finding what field is needed to make a system have some desired observable (for example, the expectation value of current in a solid). The tracking control method is attractive in being efficient and generic, applicable for closed as well as open systems. McCaul et al. formulate specific constraints with which the tracking control method guarantees the unique evolution of the system for any desirable expectation value.
The example considered in this work is an exciting proof of principle of what is possible in spectral mimicry in solid-state systems. But there are still questions to answer. For example, the researchers found that while it is possible for an insulator spectrum to mimic a conductor spectrum, the driving field forced the insulator to undergo a phase transition to a conducting state. It remains to be seen whether this spectral mimicry is possible without one of the systems making a phase transition into the phase of the other one. Even then, the researchers’ approach is still useful because it prescribes the field that’s needed to get the desired behavior. Another remaining question is whether this method of tracking control can be applied beyond the 1D Fermi-Hubbard toy model, looking instead at HHG in real solid-state systems—a topic of great current interest in the HHG community [7, 8].
Discoveries in coherent control are directly connected to a grander vision in the fundamentals of optics—to induce any desired optical response, both linear and nonlinear, in solid-state materials. One could envision the design of both a steady-state response and a transient response, allowing the creation of “out-of-equilibrium optical media.” An application of this idea is to apply new methods of coherent control to the recently reported phenomenon of light-induced superconductivity, where the optical response of a system could mimic that of a superconductor when exposed to a strong infrared optical field [9, 10].
Finally, it would be of great interest to consider coherent control with quantized driving fields, rather than classical driving fields, possibly allowing the use of coherent control to facilitate the generation of new quantum states of light [11]. With this in mind, future work could significantly extend the range of applications of tracking control and general coherent control methods into the area of quantum optics.
This research is published in Physical Review Letters and Physical Review A.
References
- M. Kac, “Can one hear the shape of a drum?” Am. Math. Mon. 73, 1 (1966).
- G. McCaul et al., “Driven imposters: Controlling expectations in many-body systems,” Phys. Rev. Lett. 124, 183201 (2020).
- G. McCaul et al., “Controlling arbitrary observables in correlated many-body systems,” Phys. Rev. A 101, 053408 (2020).
- A. G. Campos et al., “How to make distinct dynamical systems appear spectrally identical,” Phys. Rev. Lett. 118, 083201 (2017).
- P. B. Corkum, “Plasma perspective on strong field multiphoton ionization,” Phys. Rev. Lett. 71, 1994 (1993).
- W. Zhu and H. Rabitz, “Quantum control design via adaptive tracking,” J. Chem. Phys. 119, 3619 (2003).
- S. Ghimire et al., “Observation of high-order harmonic generation in a bulk crystal,” Nat. Phys. 7, 138 (2010).
- N. Tancogne-Dejean et al., “Impact of the electronic band structure in high-harmonic generation spectra of solids,” Phys. Rev. Lett. 118, 087403 (2017).
- D. Fausti et al., “Light-induced superconductivity in a stripe-ordered cuprate,” Science 331, 189 (2011).
- M. Mitrano et al., “Possible light-induced superconductivity in K3C60 at high temperature,” Nature 530, 461 (2016).
- A. Gorlach et al., “On the quantum-optical nature of high harmonic generation,” arXiv:1910.13791.