Sampling Photons to Simulate Molecules
In 2019, researchers claimed they had achieved an important milestone in quantum computing—the demonstration that a programmable quantum computer can outperform the most powerful classical computer in a specific task [1]. Using Google’s 53-qubit Sycamore quantum processor, they carried out, in just over three minutes, a “sampling” operation that could have taken, according to their estimates, thousands of years on a classical supercomputer. The task, which consisted of sampling the outputs of a random quantum circuit, had previously been identified as a promising testbed for demonstrating this quantum superiority [2]. Alas, sampling isn’t generally linked to applications of any practical relevance. Now, experiments by Christopher Wang at Yale University and colleagues show that a superconducting quantum device manipulating microwave photons can tackle a useful sampling problem—determining the so-called vibronic spectra of small molecules [3]. While the scheme doesn’t yet achieve a quantum advantage, it holds great potential for doing so if further scaled up.
In a vibronic transition, the absorption of a photon by a molecule results in the simultaneous change of both vibrational and electronic energy levels. These transitions are relevant to many important photoinduced molecular processes, including light absorption and emission, photoelectron emission, and Raman scattering. Theoretically, the intensities of these transitions depend on Franck-Condon factors, which quantify the transition probability based on the overlap between the wave functions of the initial and final vibrational states. While there is no definitive mathematical proof that a classical computer can’t reliably calculate these quantities, we know that classical algorithms are inefficient at this task. The difficulty stems from the fact that each vibrational mode of a molecule can’t be considered as an ideal, independent harmonic oscillator—one mode might be coupled to several other modes, for instance. As a consequence, computational complexity rises rapidly with the number of atoms, and even relatively small molecules can be hard to model.
In 2014, Harvard University researchers proposed that the computation of vibronic spectra can be viewed as a sampling problem, which could be simulated with a quantum setup [4]. The result was based on an approach developed in 1977 by theorist Evgeny Doktorov and co-workers, who showed that three physical processes involved in the vibronic transition—molecular structural deformation, vibrational frequency changes, and mixing of vibrational modes—can be interpreted in terms of three quantum optical operators: displacement, squeezing, and rotation, respectively [5]. Using this approach, the Harvard team showed that calculating the vibronic spectrum of a molecule is equivalent to solving a “boson sampling” task [4]. Boson sampling consists in sampling the probability distribution of photons at the output of an optical network.
This idea inspired experimental implementations both with a quantum optical setup [6, 7] and with trapped ions [8]. However, scaling up these quantum simulators to solve meaningful problems faces formidable challenges. Specifically, it requires the generation of hard-to-prepare squeezed states—in which quantum fluctuations in the photon number are reduced compared to conventional coherent light—as well as the simultaneous measurement of the quantum states of a large number of photons.
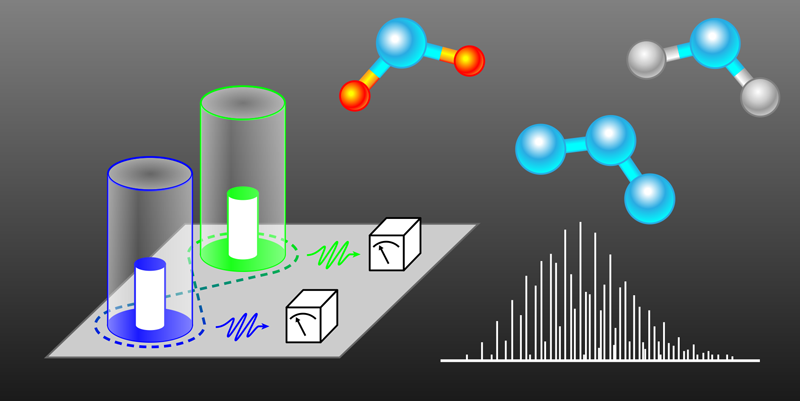
Following previous theoretical work [9], Wang and co-workers have now demonstrated experimentally another approach to vibronic-spectra computation based on superconducting microwave circuits. This solution overcomes most of the above-mentioned hurdles by exploiting the remarkable degree of control and tunability of superconducting microwave circuits. Their quantum simulator design consists of an array of superconducting microwave cavities, or resonators, each of which is coupled to the others through so-called transmon qubits (Fig. 1). These qubits allow the researchers to fine-tune the coupling between the resonators. Loosely speaking, each resonator represents one vibrational mode of a molecule, while the tunable coupling mimics the interaction between the modes.
In their proof-of-principle demonstration, the researchers used the photonic modes of two coupled superconducting resonators to simulate the photoelectron spectra of several simple triatomic molecules: water, ozone, nitrogen dioxide, and sulfur dioxide. By driving the transmon qubit at the appropriate frequencies, the researchers produced an interaction between resonators that implemented the rotation, displacement, and squeezing operations necessary to implement the Doktorov approach.
To reconstruct the Frank-Condon profiles of the molecules, the researchers needed to sample the photons in each of the resonators without perturbing them. To do so, they improved a previous quantum nondemolition (QND) scheme. In the scheme, a photon in a cavity can be measured nondestructively through the effect it has on the transition frequency of an “ancillary” qubit coupled to the cavity [10]. This method has proven to work well with single photons but, so far, could not measure larger photon numbers. To address this issue, Wang and collaborators came up with a clever alternative: Using sequential QND measurements, they managed to resolve up to 15 photons in each of the resonators. This number is way beyond what was possible in previous photonic and trapped ion platforms, allowing the device to carry out a task that was challenging for previous simulators—simulating the vibronic spectra of molecules that are in vibrationally excited states.
The current capabilities of this quantum simulator are still far from surpassing those of classical computers for this particular chemistry problem, as the spectra for these triatomic molecules can be calculated more precisely and rapidly with conventional methods. But one can expect that further advances in superconducting circuit technology will soon allow for much more interesting simulations. If the number of anharmonically coupled resonators could be increased to more than ten, for instance, the scheme could already simulate molecules that are challenging for classical computations. More sophisticated circuits could also account for effects that are extremely hard to model classically. First, a tailored photon loss mechanism in the circuit could mimic dissipation in real molecules. Second, Kerr nonlinearity—the dependence of the refractive index on light intensity—could be introduced in the setup to simulate the anharmonic effects that lead to high-order correlations between vibrational modes. With these improvements, the setup could allow researchers to simulate a wealth of molecular processes and effects that are often beyond the reach of classical simulations, including non-Condon transitions, resonant Raman scattering, multiphoton processes, vibrational circular dichroism, conical intersections, open quantum dynamics, and many others.
This research is published in Physical Review X.
References
- F. Arute et al., “Quantum supremacy using a programmable superconducting processor,” Nature 574, 505 (2019).
- S. Aaronson and A. Arkhipov, “The computational complexity of linear optics,” Proc. ACM STOC 2011 (2011); S. Boixo et al., “Characterizing quantum supremacy in near-term devices,” Nat. Phys. 14, 595 (2018).
- C. S. Wang et al., “Efficient multiphoton sampling of molecular vibronic spectra on a superconducting bosonic processor,” Phys. Rev. X 10, 021060 (2020).
- J. Huh et al., “Boson sampling for molecular vibronic spectra,” Nat. Photon. 9, 615 (2015).
- E. V. Doktorov et al., “Dynamical symmetry of vibronic transitions in polyatomic molecules and the Franck-Condon principle,” J. Molec. Spectrosc. 64, 302 (1977).
- W. R. Clements et al., “Approximating vibronic spectroscopy with imperfect quantum optics,” J. Phys. B 51, 245503 (2018).
- C. Sparrow et al., “Simulating the vibrational quantum dynamics of molecules using photonics,” Nature 557, 660 (2018).
- Y. Shen et al., “Quantum optical emulation of molecular vibronic spectroscopy using a trapped-ion device,” Chem. Sci. 9, 836 (2018).
- B. Peropadre et al., “Proposal for microwave boson sampling,” Phys. Rev. Lett. 117, 140505 (2016).
- B. R. Johnson et al., “Quantum non-demolition detection of single microwave photons in a circuit,” Nat. Phys. 6, 663 (2010).