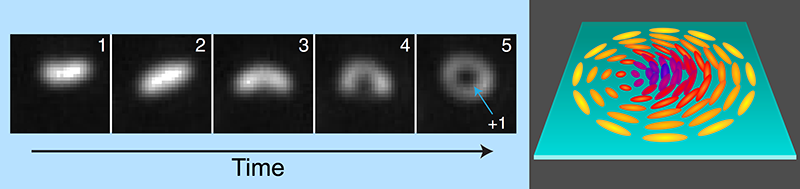
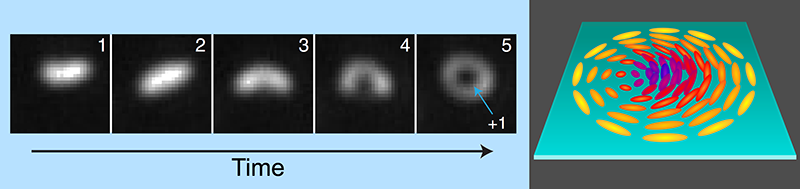
Witnessing the Birth of Skyrmions
A skyrmion is a topologically stable, vortex-like field configuration that cannot be smoothly morphed to a uniform state [1]. First proposed by physicist Tony Skyrme in 1961 as a model of the nucleon [2], the concept has since been studied in condensed-matter physics and adjacent fields [3]. In particular, skyrmions have cropped up in studies of magnetism [4], Bose-Einstein condensates [5], quantum Hall systems [6], liquid crystals [7], and in other contexts (see, for example, Viewpoint: Water Can Host Topological Waves and Synopsis: Skyrmions Made from Sound Waves). Skyrmions exhibit fascinating properties such as small size, stability, and controllability, which give them great potential for applications in spintronics, data storage, and quantum computing. Despite extensive investigations in various systems, real-time observations of skyrmion formation have been hard to achieve because of their fast dynamics and the narrow range of experimental conditions under which they are generated. Now Jaka Pišljar at the Jozef Stefan Institute in Slovenia and his collaborators have witnessed the formation of fractional skyrmions—specifically, half-skyrmions—in a chiral liquid crystal [8].
Liquid crystals (LCs) have recently garnered interest among researchers investigating skyrmions due to these systems’ inherent advantages over other media, in particular regarding experimental accessibility. LCs can, for example, be observed directly under an optical microscope, and they can be manipulated through thermal phase transitions. These properties mean that topological phenomena and the conditions that give rise to them can be easily generated and characterized. Of these conditions, a critical one is chirality: to yield skyrmions, the LC must consist of molecules with a distinct “handedness.” Such molecules stack with a slight twist between each one, forming helical structures whose orientations vary with height, like spiral staircases. In this context, skyrmions are topological structures within the array of helices—regions where the symmetry of the surrounding order is broken by a local deviation in field orientation—and they form during the transition from the LC’s isotropic phase to its helically structured phase. Much research has been conducted into generating and controlling skyrmions in chiral LCs [7], but how these complex three-dimensional structures form spontaneously is still unclear.
Pišljar and co-workers performed a series of experiments in which a chiral LC film is sandwiched between two nonparallel glass surfaces such that the thickness of the LC film varies from ∼30 to a few 100 nm. These glass surfaces were coated with polymethyl methacrylate to provide a planar-degenerate anchoring condition, meaning that surface interactions had minimal influence on the order adopted by the LC. The researchers used two LC formulations with pitches of 360 and 710 nm (the pitch defines the length that the helical structure must have in order for its orientation to complete one full rotation). They used a diffraction-limited optical microscope with an optical resolution of ∼150 nm to observe the texture of the LC as it cooled through the transition from its isotropic phase to its structured phase.
This transition is not a simple one. Between the isotropic phase and the final, fully ordered configuration, a cooling LC passes through a range of intermediate nematic states called blue phases (named for their characteristic reflective properties). In one of these intermediate phases—the so-called blue phase I (BPI)—Pišljar and co-workers directly observed the formation of topological structures called half-skyrmions. Whereas a full-skyrmion represents a full 360-degree radial rotation of the field orientation from the center to the periphery, in a half-skyrmion the field rotates by 180 degrees [7].
The team observed clusters of these half-skyrmions forming in thicker regions of the LC film ( ∼90 nm) just after it had passed the isotropic–BPI transition. The topological features originated as elongated domains in which the local field orientation differed from that of the surroundings. These domains then curved to resemble crescent moons and carried on bending until their ends met, at which point they resembled ring doughnuts about 100–300 nm across (Fig. 1). Where the film was thinner than 70 nm, stable half-skyrmions didn’t form. There, Pišljar and co-workers observed bright, round domains flickering due to the doughnut-like half-skyrmions spontaneously changing into the moon-like form, or vice versa.
Using differential dynamic microscopy, which measures changes in a material based on the intensity of scattered light, the team determined that the half-skyrmions fluctuated at a rate of ∼101–102 Hz. These dynamics are much slower than those of the nematic order parameter—a measure of the order of the LC—which fluctuates at around 106 Hz near the isotropic–BPI transition. Pišljar and co-workers explain the difference in these fluctuation rates by calculating the times for hopping between the two symmetry-broken free-energy minima, which represent the paranematic (moon-shaped) or skyrmion (doughnut-shaped) structures, separated by small energy barrier. Finally, they show that this fluctuation not only breaks the continuous symmetry of the disordered phase but also—because the moon-shaped and doughnut-shaped features have topological charges of 0 and 1, respectively—changes the topology of the orientational field. This is surprising, as topological charge is a conserved quantity, and the orientational field is therefore expected to be topologically charge neutral at all times. The researchers show that, as the LC cools out of this transitional regime, stable half-skyrmions form in large numbers and then merge together, restoring topological charge neutrality.
The demonstration by Pišljar and co-workers that skyrmion fluctuations can be observed in very thin LC films offers a new approach for studying the real-time dynamics of the formation of topological solitons such as skyrmions, hopfions, and twistions, which are topologically nontrivial configurations with knotted nematic fields in LCs [9]. Their research will provide valuable perspectives on studying fundamental properties of such topological entities and of topological phase transitions that occur in various soft-matter and magnetic systems, with applications extending to many fields, including magnetism, spintronics, and topology.
References
- J. Wu and I. I. Smalyukh, “Hopfions, heliknotons, skyrmions, torons and both abelian and nonabelian vortices in chiral liquid crystals,” Liq. Cryst. Rev. 10, 34 (2022).
- T.H.R. Skyrme, “A unified field theory of mesons and baryons,” Nucl. Phys. 31, 556 (1962).
- B. Göbel et al., “Beyond skyrmions: Review and perspectives of alternative magnetic quasiparticles,” Phys. Rep. 895, 1 (2021).
- S. Mühlbauer et al., “Skyrmion lattice in a chiral magnet,” Science 323, 915 (2009).
- U. A. Khawaja and H. Stoof, “Skyrmions in a ferromagnetic Bose–Einstein condensate,” Nature 411, 918 (2001).
- S. L. Sondhi et al., “Skyrmions and the crossover from the integer to fractional quantum Hall effect at small Zeeman energies,” Phys. Rev. B 47, 16419 (1993).
- J. Fukuda and S. Žumer, “Quasi-two-dimensional Skyrmion lattices in a chiral nematic liquid crystal,” Nat. Commun. 2, 246 (2011); D. Foster et al., “Two-dimensional skyrmion bags in liquid crystals and ferromagnets,” Nat. Phys. 15, 655 (2019); J. B. Tai and I. I. Smalyukh, “Surface anchoring as a control parameter for stabilizing torons, skyrmions, twisted walls, fingers, and their hybrids in chiral nematics,” Phys. Rev. E 101, 042702 (2020); G. Park et al., “Fabrication of arrays of topological solitons in patterned chiral liquid crystals for real-time observation of morphogenesis,” Adv. Mater. 34 (2022).
- J. Pišljar et al., “Dynamics and topology of symmetry breaking with skyrmions,” Phys. Rev. Lett. 132, 178101 (2024).
- P. J. Ackerman and I. I. Smalyukh, “Diversity of knot solitons in liquid crystals manifested by linking of preimages in torons and hopfions,” Phys. Rev. X 7, 011006 (2017).