Susceptible to Pairing

Dirk van der Marel; Jason N. Hancock

Viewpoint

Susceptible to Pairing

Département de Physique de la Matière Condensée, Université de Genève, quai Ernest-Ansermet 24, CH 1211 Genève 4, Switzerland

October 31, 2011• Physics 4, 89

The theoretical prediction of the frequency and temperature dependent tendency toward Cooper pairing in five different scenarios allows experimental identification of mechanisms of superconductivity.

Figure caption — **Figure 1:** (Left) To carry out future experiments on quantum critical superconductors as proposed by She *et al.* [2], a two-layer tunnel junction could be used that consists of a high-transition-temperature superconductor (HTSC) next to a low-transition-temperature superconductor in the normal state (LTSC). The two layers are separated by a thin insulating barrier. In the HTSC all the electrons are paired (colors indicate spins), whereas in the LTSC some of the Cooper pairs can tunnel into the normal material from the superconductor. This effect is larger when the pair susceptibility increases as indicated by the tunneling current. (Right) Experimental measurements of the pair susceptibility could distinguish between conventional BCS behavior (top curve) and exotic quantum critical superconductivity (bottom panel).

One mole ( $N_{A}$ ) of identical hikers starts from Geneva for a trip through the mountains to the Mediterranean Sea. Before they start, they have to pick their mountain boots from a heap of $2 N_{A}$ left and right boots. They are in a hurry to leave, and each one picks a pair at random from the heap, resulting in approximately $N_{A} / 4$ hikers with two left boots, $N_{A} / 4$ who have two right boots, and the remaining ones who have one left and one right boot. Obviously for half of them walking is a painful affair and they are never going to make it to the first mountain hut before dinner time, so they start trading. After a while everyone ends up with a proper pair of boots (one left and one right), the going is now easy, and they all arrive in time for a serving of tartiflettes, the tasty local cheese and potato gratin.

Similar mechanisms are at work in the phenomenon of superconductivity, the lossless flow of electrical current discovered $100$ years ago by Kamerlingh Onnes [1]. Since the 1930s, we have known that this is a macroscopic quantum state of charged particles, constituting a spectacular manifestation of quantum physics on a truly macroscopic scale. Electrons are enslaved by the Pauli exclusion principle, forcing them all into different quantum states. Since electron pairs have statistical properties similar to those of bosons, a macroscopic number of them are allowed to form a condensate, which corresponds to the superconducting state. This is the Bardeen-Cooper-Schrieffer (BCS) model in a nutshell, except for one crucial ingredient: the mechanism binding electrons into pairs. In a paper in Physical Review B, Jian-Huang She and colleagues at the University of Leiden, The Netherlands, present their theoretical analysis of novel ways that such mechanisms might be experimentally tested in unconventional superconductors [2].

In the early 1950s, David Pines and John Bardeen [3] established that the combination of Thomas-Fermi screening and electron-phonon interaction can overcome the Coulomb repulsion, leading to an attractive interaction that binds electrons into pairs. However, electron-phonon-mediated interaction in a Fermi liquid is not the only way to form pairs; superfluid $^{3} He$ is a good example. Moreover, many materials are known where superconductivity occurs in close proximity to, or even coexisting with, a magnetically ordered state [4–6]. Since, from the BCS perspective, magnetic order and superconductivity are antagonistic phenomena, this poses a serious challenge to the standard model of superconductivity. By tuning the magnetic state to zero through control of some parameter (pressure, magnetic field, or stoichiometry), superconductivity is stabilized exactly at the quantum critical point where the magnetic order vanishes. These observations offer a tantalizing and inspiring clue for which a variety of interpretations have been given [2].

She and Jan Zaanen [7] have, for example, proposed in a seminal paper a model where, due to quantum critical fluctuations, the pair susceptibility (i.e., the linear response of the pair amplitude to the pairing field) takes the form of a power law as a function of frequency, similar to the optical conductivity [8]. The quantum critical susceptibility makes electrons “prone to pair,” and a weak, garden variety, electron-phonon interaction can easily tip the balance to the superconducting state, even at relatively high temperatures. The essentials are aptly captured by the slogan “more bang for your buck.” Earlier approaches took phenomenological models of the normal state as a starting point. The normal state is assumed to be a quantum critical non-Fermi-liquid in some models, and a Fermi liquid in others. The influence of quantum criticality is a bit like that of the mountainous terrain in that it is underlying, and tips the balance toward pairing rather rapidly. On flat ground, the “hiker fermions” could go further before pairing.

Now, She et al. [2] lay out in parallel the theoretical expectations for the pair susceptibility of $5$ different theories of superconductivity in quantum critical metals. These scenarios include the orthodox BCS theory with a simple Einstein-oscillator pairing function, BCS with a Hertz-Millis-type criticality of the bosonic spectrum, BCS with a simple pairing function and quantum critical electrons, and two limits of the recently developed holographic superconductivity that borrow mathematical concepts from string theory [anti–de Sitter/conformal field theory (AdS/CFT) correspondence] in order to handle scaling near a quantum critical point.

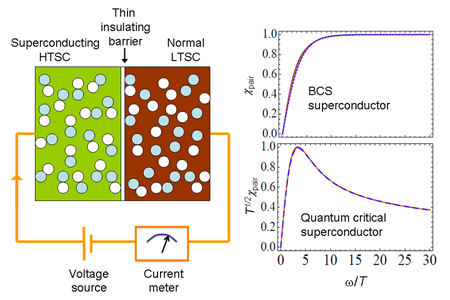
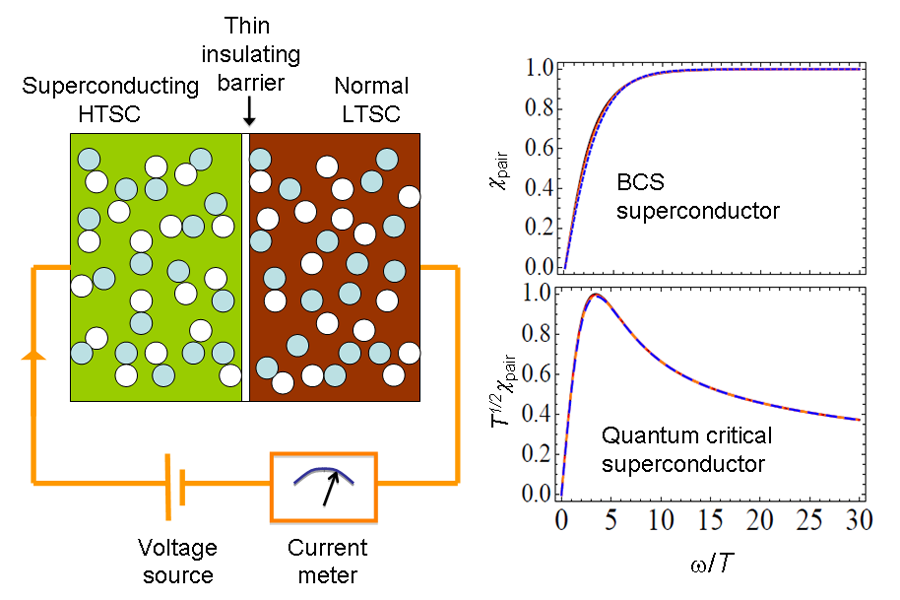
The pair susceptibility shows a distinct signature in each case considered, suggesting that a measurement of $χ_{pair} (ω, T$ ) could distinguish among theoretical proposals (Fig. 1). In contrast to many bulk properties like electrical transport and magnetometry, which can be related to integral convolutions over $χ_{pair} (ω$ ), a direct measurement of this quantity sharpens the contrast between various theories.

A method for measuring $χ_{pair} (ω, T$ ) was suggested by Ferrell [9] and developed in 1970 by Scalapino [10]. The experiment involves creation of a thin insulating junction between two superconductors with very different transition temperatures, $T_{c}^{high}$ and $T_{c}^{low}$ . At temperatures $T_{c}^{low} < T < T_{c}^{high}$ and at fixed voltage $V$ across the junction, the current is not simply determined from Ohm’s law and the serial sum of the bulk resistances of the layers, but there is an “extra” current that arises from the influence of the high- $T_{c}$ condensate on the lower- $T_{c}$ material, still in its normal state. The extra current that flows is determined by the lower- $T_{c}$ material’s propensity to accept Cooper pairs from the higher- $T_{c}$ neighbor, i.e., $χ_{pair} (ω, T$ ). The excess current therefore constitutes a direct measurement of the pair susceptibility at a frequency related to the voltage drop across the barrier $ω = 2 e V / ħ$ .

Creating a junction with appropriate characteristics and sufficient quality is itself an achievement, and an essential prerequisite to the proposal of She et al. [2]. The first experiment of this type was successfully performed in conventional superconductors by Anderson and Goldman [11] in the same year as Scalapino’s proposal. This measurement required careful elimination of a possible extraneous signal that may be confused with the desired “extra current” through the junction. Related challenges were overcome by development of masking techniques to avoid extraneous signals near the higher- $T_{c}$ strained edges of the sample, systematic tests for possible shortcuts through the insulating barrier, and magnetic field tests to steer clear of a regime where a known thermal effect on the dc Josephson coupling could give an unwanted additional signal [12]. With these influences under control, the excess current above the quasiparticle contribution was found, consistent with prediction.

To apply this technique to unconventional superconductors with a pairing symmetry different from $s$ wave, new technical difficulties arise due to enhanced contributions from quasiparticle tunneling. However, such an experiment was recently performed successfully in an underdoped cuprate superconductor [13]. This measurement suggested that pairing fluctuations persist over only a narrow temperature window above $T_{c}$ , but, importantly for the work of She et al. [2], showed that Scalapino’s suggestion could indeed be performed in practice on an unconventional superconductor.

The pair susceptibility is the quantity most central to superconductivity. The proposed experimental mapping of $χ_{pair} (ω, T$ ) as a function of frequency and temperature, while difficult, is within reach of state-of-the art technology. She et al. have demonstrated theoretically that such maps provide invaluable insight into the inner workings of superconductivity. Experimentalists, be forewarned: the trail to this mountain is steep and sinuous; suitable boots come in pairs.

References

100 Years of Superconductivity,edited by Horst Rogalla and Peter H. Kes (Taylor & Francis, New York, 2011)
J-H. She, B. J. Overbosch, Y-W. Sun, Y. Liu, K. E. Schalm, J. A. Mydosh, and J. Zaanen, Phys. Rev. B 84, 144527 (2011)
D. Pines and J. Bardeen, Phys. Rev. 99, 1140 (1955)
H. W. Meul, C. Rossel, M. Decroux, Ø. Fischer, G. Remenyi, and A. Briggs, Phys. Rev. Lett. 53, 497 (1984)
D. Jaccard, K. Behnia, and J. Sierro, Phys. Lett. A 163, 475 (1992)
J. L. Tallon, and J. W. Loram, Physica C 349, 53 (2001)
J.-H. She and J. Zaanen, Phys. Rev. B 80, 184518 (2009)
D. van der Marel, H. J. A. Molegraaf, J. Zaanen, Z. Nussinov, F. Carbone, A. Damascelli, H. Eisaki, M. Greven, P. H. Kes, and M. Li, Nature 425, 271 (2003)
R.A.Ferrell, J. Low Temp. Phys. 1,423 (1969)
D. J. Scalapino, Phys. Rev. Lett. 24, 1052 (1970)
J. T. Anderson and A. M. Goldman, Phys. Rev. Lett. 25, 743 (1970)
J. T. Anderson and A. M. Goldman, Phys. Rev. Lett. 23, 128 (1969)
N. Bergeal, J. Lesueur, M. Aprili, G. Faini, J. P. Contour, and B. Leridon, Nat. Phys. 4, 608 (2008)

About the Authors

Dirk van der Marel has been a professor of physics in the Condensed Matter Physics Department at the University of Geneva since 2003. He received his Ph.D. in 1985 at the University of Groningen. After postdoctoral research at Philips Research Laboratories, he went on to become an assistant professor at the University of Delft and, in 1992, a full professor at the University of Groningen. He has been a visiting scientist at the Max Planck Institute in Stuttgart and at Stanford University. His research interests include optical spectroscopy and electronic properties of strongly correlated electron systems. In 2016, he received the APS Frank Isakson prize for optical effects in solids.

Jason Hancock is a postdoctoral fellow at the University of Geneva. He completed a Ph.D. degree in 2004 at the University of California Santa Cruz, where he used infrared spectroscopy to study the hybridization gap in heavy fermions and lattice vibrations responsible for negative thermal expansion. During postdoctoral research at Stanford University, he worked on foundations of the resonant inelastic x-ray scattering (RIXS) technique and its application to cuprate superconductors. His recent research directions involve the use of photon-based spectroscopies to study charge dynamics in strongly correlated and topological quantum materials.