Cooper Pairs Dance in a Disk
Physicists like to play with dimensions and hunt for surprises in 1D and 2D worlds. In solids, for example, reducing the number of dimensions—say, by making a crystal whose electrons move only in a plane—disrupts the natural tendency of matter to order at low temperatures. This hindrance to order comes from thermal fluctuations, which are stronger in 1D and 2D systems than in 3D systems. But in the 1970s, Berezinskii, Kosterlitz, and Thouless (BKT) discovered a mechanism that, in certain 2D systems, tames fluctuations [1,2] and allows “quasi”-long-range order, in which correlations fall off much more slowly than in a disordered phase. Now, experiments with cold fermionic atoms in a disk-shaped trap explore the effect of the BKT mechanism on the superfluid phase transition of paired-fermions (Cooper pairs), a system of potential interest to understanding the physics of high-temperature superconductors [3,4]. In their experiments, Martin Ries and colleagues at the University of Heidelberg, Germany, cool the paired atoms to low temperatures and utilize specialized techniques to determine the onset temperature for superfluidity, a frictionless phase of neutral particles analogous to superconductivity of electrons.
High-temperature (high- ) cuprate superconductors are nearly two-dimensional fermionic systems. They are notoriously difficult to describe theoretically because there is no consensus as to what basic mechanism explains their unusual electrical, magnetic, and optical properties. As a result, different schools of thought exist about which “simple” models best describe them as a whole. Even these “simple” models turn out to be difficult to solve, and theorists must resort to approximation methods that are difficult to validate.
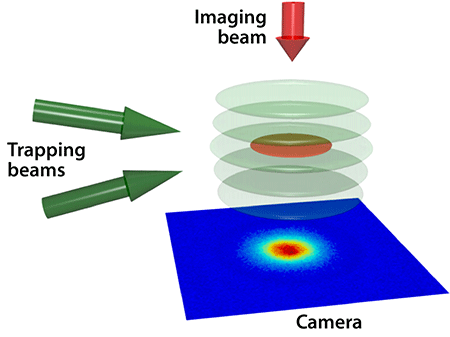
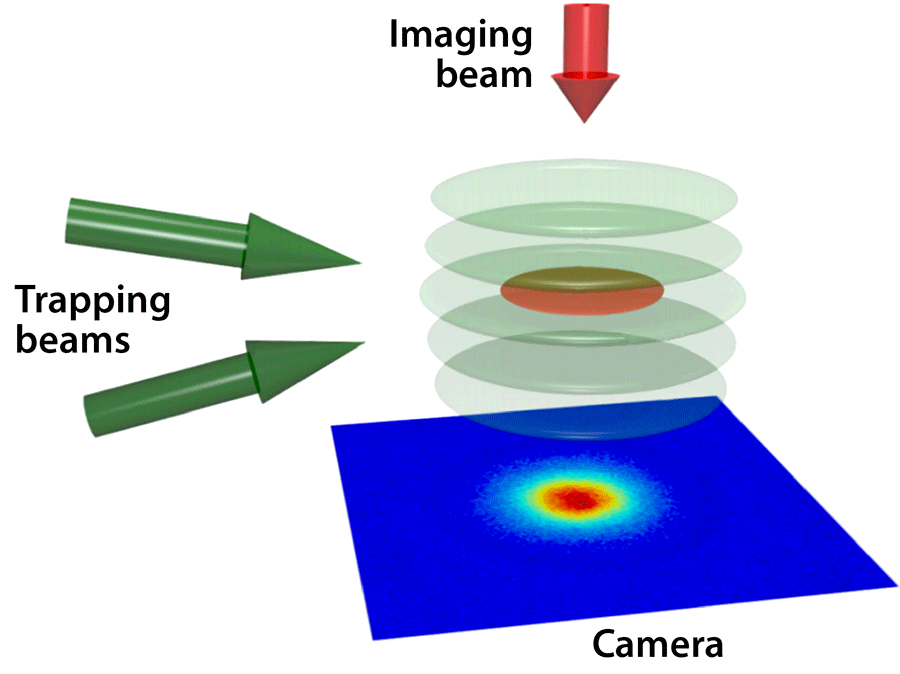
The system of atoms studied by Ries et al. mimics the simplest model for 2D superconductors: fermions interacting through a short-range attraction. The researchers create the 2D gas by loading ultracold fermionic lithium-6 atoms into a standing-wave trap created by two interfering laser beams. The lasers exert a force 300 times stronger along the vertical direction of the trap compared with the in-plane direction, forcing most of the atoms to move within a flat disk (Fig. 1). The researchers use a magnetic field to control an effective attraction between the atoms in two different hyperfine levels, a technique known as a Fano-Feshbach resonance. In this way, they can explore two distinct regimes: one with strongly paired fermions, which behave like bosonic “molecules” that, when cooled, can form a Bose-Einstein condensate (BEC); and a regime with weakly paired fermions, like the Cooper pairs in the Bardeen-Cooper-Schrieffer (BCS) theory of superconductivity. Tuning the Fano-Feshbach resonance allows the researchers to span the so-called BCS-BEC crossover, where one regime evolves smoothly into the other (see 27 January 2014 and 23 January 2012 Viewpoints). Theorists believe the crossover region, where the pairs are relatively tightly bound, is potentially relevant to high- superconductors.
Even in 3D, this crossover region is difficult to describe theoretically because approaches that describe bosonic molecules on the BEC side do not adequately describe the weakly paired fermions on the BCS side, and vice-versa. In 2D, the problem is further complicated because the BKT mechanism comes into play. As a consequence, theory cannot reliably calculate the superfluid phase transition temperature through the 2D BCS-BEC crossover. This temperature is precisely what Ries et al. measure.
The key experimental challenge for Ries et al. was devising techniques to measure the superfluid transition in the atom gas. In general, the signature of superfluidity in a cold gas of bosonic atoms is a change in the distribution of the atoms’ momenta relative to that of atoms in a thermal gas. Specifically, there are a significantly larger fraction of atoms with low momenta. To detect this different distribution, researchers normally rely on a “time-of-flight” measurement, which consists of releasing the atoms from their trap, letting them expand for a known length of time, and detecting their final positions with absorption spectroscopy. Since fast atoms travel further than slow ones, the spread in final positions is a snapshot of the atoms’ momenta at the time the trap was released.
Unlike bosonic atoms, however, which are well-defined particles, paired fermions result from many-body effects and can flit in and out of existence. To determine the momenta of these correlated pairs, the authors therefore used a technique first developed for 3D fermionic gases. The idea is to quickly sweep the Fano-Feshbach resonance so the paired fermions form more tightly bound molecules whose momenta can be measured directly [5].
A second challenge relates to the BKT-nature of the transition, which makes the shift in the atoms’ momenta at the superfluid transition more difficult to discern than in 3D systems. The shift is most significant at zero momentum, but this is, unfortunately, the region where the time-of-flight method is least accurate. (Slow atoms travel only a short distance in a time-of-flight experiment, so the error from assuming they started at the center of the trap can be large.) Ries et al. therefore utilized a so-called “focusing” approach, originally developed for 2D bosonic atoms [6]. The idea is to release the gas from its trap and then subject it to a weak 2D harmonic potential. In the same way that a pendulum will swing through its center at one quarter of a period if it’s released with zero velocity, fermions with zero velocity will focus at the center of the harmonic trap. The researchers can pinpoint the onset of the superfluid phase by using absorption spectroscopy (and the projection method described above) to detect an increase in the number of molecules at the center of the trap. Ries et al. measured as they increased the pairing interaction between the fermions, allowing them to explore the BCS to BEC crossover regime [3]. In a separate paper [4], they used the same momentum distributions to determine the correlations between paired fermions, confirming quasi-long-range order in the superfluid phase and thus the BKT nature of the transition.
Phase transitions involving the BKT mechanism have been seen in other systems, including helium- atoms in a thin liquid film [7], granular superconductors [8], and, more recently, ultracold bosonic atoms [9]. But the system studied by Ries et al. is the first one that allows the BKT transition to be observed and tested with trapped fermions. And since fermions (in the form of electrons) are the main actors in materials, such experimental tests are particularly relevant to solid-state physics. Knowing the critical temperature across the 2D BCS-BEC crossover will allow physicists to validate or challenge calculations of this quantity. And it feeds experimentalists and theorists with a crucial quantity—an effective energy scale—that can be used to gauge the importance of other parameters (such as the pairing pseudogap [10]) in the 2D BCS-BEC crossover.
This research is published in Physical Review Letters.
References
- V. L. Berezinskii, “Destruction of Long-Range Order in One-Dimensional and Two-Dimensional Systems Possessing a Continuous Symmetry Group. II. Quantum Systems,” Sov. Phys. JETP 34, 610 (1972)
- J. M. Kosterlitz and D. J. Thouless, “Ordering, Metastability and Phase-Transitions In Two-Dimensional Systems,” J. Phys. C 6, 1181 (1973)
- M. G. Ries, A. N. Wenz, G. Zürn, L. Bayha, I. Boettcher, D. Kedar, P. A. Murthy, M. Neidig, T. Lompe, and S. Jochim, “Observation of Pair Condensation in the Quasi-2D BEC-BCS Crossover,” Phys. Rev. Lett. 114, 230401 (2015)
- P. A. Murthy, I. Boettcher, L. Bayha, M. Holzmann, D. Kedar, M. Neidig, M. G. Ries, A. N. Wenz, G. Zürn, and S. Jochim, “Observation of the Berezinskii-Kosterlitz-Thouless Phase Transition in an Ultracold Fermi Gas,”arXiv:1505.02123
- C. A. Regal, M. Greiner, and D. S. Jin, “Observation of Resonance Condensation of Fermionic Atom Pairs,” Phys. Rev. Lett. 92, 040403 (2004)
- S. Tung, G. Lamporesi, D. Lobser, L. Xia, and E. A. Cornell, “Observation of the Presuperfluid Regime in a Two-Dimensional Bose Gas,” Phys. Rev. Lett. 105, 230408 (2010)
- D. J. Bishop and J. D. Reppy, “Study of the Superfluid Transition in Two-Dimensional He films,” Phys. Rev. Lett. 40, 1727 (1978)
- D. J. Resnick, J. C. Garland, J. T. Boyd, S. Shoemaker, and R. S. Newrock, “Kosterlitz-Thouless Transition in Proximity-Coupled Superconducting Arrays,” Phys. Rev. Lett. 47, 1542 (1981)
- Z. Hadzibabic, P. Krüger, M. Cheneau, B. Battelier, and J. Dalibard, “Berezinskii-Kosterlitz-Thouless Crossover in a Trapped Atomic Gas,” Nature 441, 1118 (2006)
- F. Marsiglio, P. Pieri, A. Perali, F. Palestini, and G. C. Strinati, “Pairing Effects in the Normal Phase of a Two-Dimensional Fermi Gas,” Phys. Rev. B 91, 054509 (2015)