Lamb Shift Spotted in Cold Gases
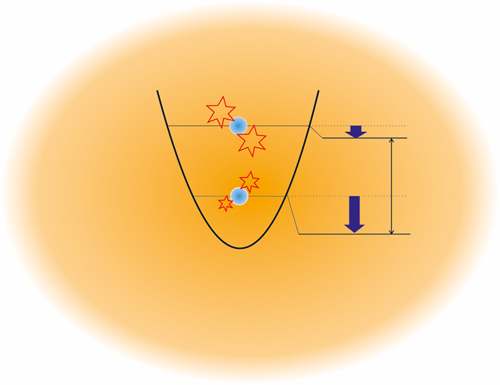
According to quantum mechanics, vacuum is not just empty space. Instead, it boils with fluctuations—virtual photons popping in and out of existence—that can affect particles embedded in it. The celebrated Lamb shift, first observed in 1947 by Willis Lamb and Robert Retherford [1], is a seminal example of this phenomenon (see 27 July 2012 Focus story). The Lamb shift is a tiny difference in energy between two levels of a hydrogen atom that should otherwise have the same energy in classical empty space (see Fig. 1). It arises because zero-point fluctuations of the electromagnetic field in vacuum perturb the position of the hydrogen atom’s single bound electron. The observation of the effect had a disruptive impact on the developments of quantum mechanics as, at the time, theory had no explanation for it.
This paradigmatic model can be applied to different physical systems. For example, we can create a solid-state analog of the Lamb shift if we replace hydrogen’s electron with an electron bound to a defect in a semiconductor, and replace the vacuum fluctuations with the bath of acoustic vibrations (phonons) that propagate in the material. Predicted several years ago [2], the observation of this phononic Lamb shift has remained elusive because of disorder-induced effects that are unavoidable in real solids. By turning instead to ultracold atoms, Tobias Rentrop and colleagues from the University of Heidelberg in Germany have now managed to observe the phononic analog of the Lamb shift, and they have provided the first quantitative measurement of the shift [3].
In recent years, ultracold atom experiments have become a sophisticated platform with which to test theoretical models. The ability to fine tune all experimental parameters, including the external potentials that confine the atoms and the interactions between particles, allows researchers to build up, piece by piece, controllable systems that would otherwise not be attainable. What’s more, these systems can be interrogated with a range of powerful diagnostic techniques, from imaging with resolution up to single-atom sensitivity, to advanced spectroscopic methods that probe the particles’ quantum states. The synthetic system built by Rentrop et al. is made of an imbalanced mixture of two different atomic species: 1000–10,000 lithium atoms and a large Bose-Einstein condensate (BEC) of about one million sodium atoms. The lithium impurities are pinned to the wells of a periodic potential formed by two interfering laser beams (a so-called optical lattice), and play the role of the bound defects. These impurities are immersed in a weakly confined BEC of sodium atoms, which provides a bath of phononic excitations. Similarly to a solid, a BEC’s low-lying energy excitations are phonons with a linear dispersion relation, analogous to the photons in the vacuum of the original Lamb shift scenario. The impurity atoms are “dressed,” in the sense that their behavior is modified by the excitations of the surrounding environment. These new entities, or quasiparticles, are called polarons, and their effective mass and mobility differs greatly from that of a bare particle. Depending on the quantum statistics of the bath, the polaron can either be a Fermi or a Bose polaron.
To model their experiments, Rentrop and co-workers modify a theory developed by Herbert Fröhlich in 1954 [4], which describes the bosonic case in the weakly interacting regime for a mobile electron in a semiconductor. They do so by accounting for the fact that the interaction of the defects with the bath arises from “contact” collisions between the atoms, rather than from the long-range Coulomb interaction of the original formulation. Additionally, because they deal with bound particles (bound polarons), they extend the model to impurities confined by the parabolic potential at each site of the optical lattice, in analogy with the electron bound to an ion in a solid or to a proton in the hydrogen atom. The validity of the Fröhlich description for the impurity-BEC scenario requires that the interaction between the impurity and the atoms in the BEC be small and that the density of impurities be low enough to avoid phonon-mediated interactions between them. The authors are able to fulfill all of the constraints of the Fröhlich model by selecting the right atomic species and using a relatively large spacing between the wells of the optical lattice.
To detect the phononic Lamb shift, the researchers measured the energy difference between the two lowest-energy motional states of the bound lithium atoms, with and without the BEC. This comparison amounts to performing a measurement with and without the quantum vacuum—an important distinction from quantum-electrodynamic (QED) or solid-state experiments, in which the vacuum cannot be removed and the properties of the bare particles cannot be accessed. This cold-atom experiment instead realizes a synthetic vacuum that can be turned on and off to probe its effect.
The measurement is performed with a novel form of Ramsey spectroscopy [5]—an atom interferometry technique for measuring transition frequencies in atoms. A first pulse creates a coherent superposition of two motional states of the atoms trapped in the lattice. This pulse, which for most atom experiments is a flash of microwave radiation or laser light, is instead realized here by shaking the optical lattice for a very short time. During a so-called “interrogation” time, a phase difference accumulates between the two states, which depends on their energy difference. A second pulse, identical to the first, measures this phase difference by determining the final occupation probability of the two states. In this way, information about the energy difference can be extracted by measuring the number of atoms in each state at the end of the sequence.
The authors measured an energy shift in the presence of the quantum vacuum, finding a value in good agreement with theoretical expectations. In addition to providing the first quantitative measurement of the phononic Lamb shift, the result confirms the validity of the theoretical framework that describes the effect. By using two different lithium isotopes, one fermionic and the other bosonic, the researchers also revealed that the two impurities exhibit a fundamentally different behavior: a larger Lamb shift is observed for bosonic particles because of the so called Bose enhancement. Contrary to fermions, bosons tend to cluster in the same quantum state, acting cooperatively in the process of phonon scattering and thereby enhancing the energy shift.
The clean experimental realization and the ingenious methodologies of this work open new avenues for the quantitative exploration of other QED phenomena. An intriguing example would be the celebrated Casimir effect. Furthermore, the experiment provides a testbed for complex many-body theories, which may help to shed light on fundamental unresolved problems such as the origin of high-temperature superconductivity.
This research is published in Physical Review X.
References
- W. E. Lamb and R. C. Retherford, “Fine Structure of the Hydrogen Atom by a Microwave Method,” Phys. Rev. 72, 241 (1947).
- P. M. Platzman, “Ground-State Energy of Bound Polarons,” Phys. Rev. 125, 1961 (1962).
- T. Rentrop, A. Trautmann, F. A. Olivares, F. Jendrzejewski, A. Komnik, and M. K. Oberthaler, “Observation of the Phononic Lamb Shift with a Synthetic Vacuum,” Phys. Rev. X 6, 041041 (2016).
- H. Fröhlich, “Electrons in Lattice Fields,” Adv. Phys. 3, 325 (1954).
- R. Scelle, T. Rentrop, A. Trautmann, T. Schuster, and M. K. Oberthaler, “Motional Coherence of Fermions Immersed in a Bose Gas,” Phys. Rev. Lett. 111, 07040 (2013).