Traveling with a Quantum Salesman
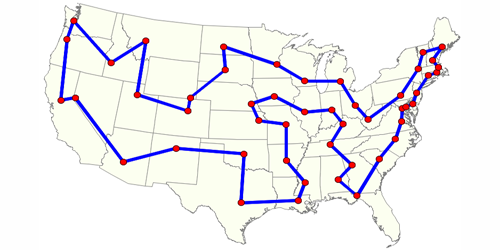
A traveling salesman may seem like a relic from a bygone era, but the emblematic problem facing this profession hasn’t gone away: what’s the shortest path for visiting multiple cities and then returning home? The traveling salesman problem (TSP) can describe many situations, such as the optimization of electric wiring or business scheduling. But it becomes computationally intense for a large number of cities or other elements. New work by Alexandra Moylett and colleagues at the University of Bristol, UK, shows how quantum computing could potentially speed up TSP algorithms.
There are several ways to help a traveling salesman pick his route. The brute force method is to compute the distance for every possible itinerary. For cities, this would involve roughly computations, which becomes astronomically large as grows. A quantum computer could provide a quadratic speedup by reducing the number of computations to . However, recent efforts have come up with “shortcut” classical algorithms that can solve the TSP with less than steps, which is significantly better than the quantum brute force treatment.
Could shortcut algorithms benefit from quantum computing? Moylett and colleagues considered a special type of shortcut involving so-called backtracking. In the classical case, one iteratively selects a road between cities, assigns it a value of “traveled on” or “not traveled on,” and then checks whether this assignment is consistent with forming a complete route through each city. For quantum backtracking, the team assigns a superposition of “traveled on” and “not traveled on” to each road and then simultaneously checks both. The results show that a near-quadratic speedup can be obtained when the number of roads leaving each city is small.
This research is published in Physical Review A.
–Michael Schirber
Michael Schirber is a Corresponding Editor for Physics based in Lyon, France.