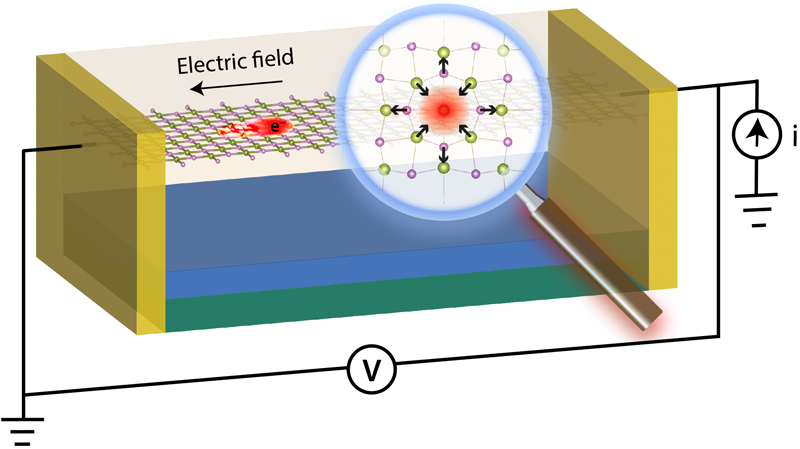
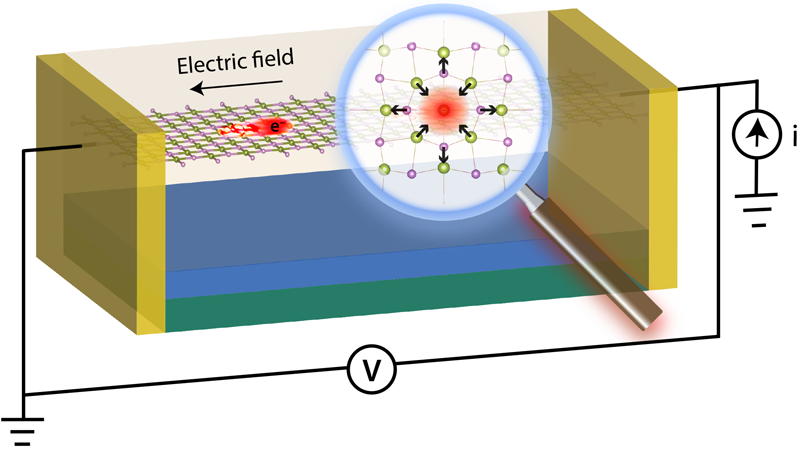
Polarons Get the Full Treatment
In 1933, theoretical physicist Lev Landau wrote a 500-word article discussing how an electron traveling through a solid might end up trapped by a distortion of the surrounding lattice [1]. Those few lines marked the beginning of the study of what we now call polarons, some of the most celebrated “quasiparticles” in condensed-matter physics—essential to understanding devices such as organic light-emitting-diode (OLED) displays or the touchscreens of smart devices. Until now, researchers have relied on two approaches to describe these complex quasiparticles: idealized mathematical models and numerical methods based on density-functional theory (DFT). On their own, each approach has limitations, but Weng Hong Sio and colleagues from the University of Oxford, UK, combined elements of the two approaches into one formalism that could dramatically boost our ability to model polarons of different types and in different materials. The new method allowed them to derive an unprecedentedly detailed picture of polarons in an ionic crystal and in an oxide used for energy storage applications [2, 3].
When an electron travels through a solid, its negative charge exerts an attractive force on the surrounding positively charged atomic nuclei. In response, the nuclei move away from their equilibrium positions, trying to reach for the electron. The resulting distortion of the crystalline lattice creates a lump of positive charge that tags along with the moving electron. This combination of the electron and the lattice distortion—which can be seen as an elementary particle moving through the solid—is a polaron [4, 5]. In the language of condensed-matter physics, the polaron is a quasiparticle formed by “dressing” an electron with a cloud of phonons, the quantized vibrations of the crystal lattice. Polarons may be large or small—depending on how the size of the lattice distortion they carry compares to the lattice constant—and tend to be effectively heavier than electrons, that is, harder to push around using electric fields.
Our current understanding of polarons has been shaped by idealized mathematical models, such as the one developed by Herbert Fröhlich in 1950 [6]. His model was introduced to study electrons moving in ionic crystals such as alkali halides. Since these crystals are polar, the atomic vibrations associated with certain optical phonons generate strong oscillating electric fields that can affect the electron’s movement. The Fröhlich model accounts for this effect by considering one electron whose wave function spreads over many ions. The electron moves within a parabolic conduction band while coupling to optical phonons. Despite the apparent simplicity of this model, its solution troubled theorists—even Richard Feynman—for more than half a century [7–9]. While these theorists’ contributions represent great feats of condensed-matter theory, Fröhlich’s model and others like it cannot account for many features of real materials—complex band structures, unit cells, and phonon dispersion curves. And they can’t tackle difficult systems like interfaces, surfaces, or low-dimensional materials.
In the past decade, researchers have explored an alternative approach—first-principles numerical calculations of polarons based on DFT [10]. The idea is to add one electron to a large subset of the crystal (a “supercell”) and find the minimum-energy state of the entire system using optimization algorithms. This strategy is useful for investigating real materials, since the supercell can be described with atomistic detail. However, there are limitations. In particular, since the computational cost of DFT scales with the third power of the number of atoms, only very small polarons can be studied. For example, the electron polaron in a simple salt like lithium fluoride (LiF) is less than a nanometer in size, but its description requires a supercell containing more than 5000 atoms. This is already at the limit of current computational capabilities; investigating larger polarons is out of the question. Another practical difficulty is related to the fact that DFT, being a mean-field theory, produces an unphysical effect on the polaron: It experiences a spurious Coulomb repulsion from its own electronic charge. In some cases, this self-interaction is sufficiently strong to destabilize the polaron, leading to incorrect predictions. Lastly, since DFT relies on the adiabatic Born-Oppenheimer approximation, it is challenging to upgrade the theory so that it accounts for quantum fluctuations of the atomic nuclei or nonadiabatic electron-phonon correlations.
Now Sio and colleagues have combined idealized polaron models and supercell DFT approaches in a single formalism [2, 3]. Their idea is to use DFT to find the ground-state energy of the polaron but to avoid explicit calculations for the entire supercell. To do this, they express all relevant quantities—the polaron’s wave function and formation energy, the atomic displacements associated with the polaron, and the effect of polarons on all the other electrons and atomic nuclei—in terms of several ingredients. These ingredients, which include the electron band structure, phonon dispersion relations, and electron-phonon coupling constants, can be evaluated within the first Brillouin zone of the reciprocal lattice. This strategy allows them to reformulate the polaron problem as a standard nonlinear optimization problem that requires DFT calculations only within one primitive cell of the crystal, rather than within a prohibitively large supercell.
The authors show that the derived polaron equations are essentially as accurate as explicit DFT calculations, while offering additional perks. Most importantly, the equations allow them to tackle systems that would have been beyond the reach of existing DFT approaches. For example, they enable, for the first time, investigation of large polarons—polarons whose radii are much larger than the unit cell of the material—with atomic-scale detail and in real materials,. What’s more, the new equations get rid of the spurious polaron self-interaction.
Sio and colleagues demonstrate the power of their approach by computing polarons in LiF and in a well-known material for lithium-ion batteries, Li2O2. Their computations deliver a close-up view of the structure of the polarons at the atomic scale. For example, the electron in LiF forms a large polaron that looks like a lump of negative charge that attracts Li+cations and repels F− anions (Fig. 1). While the obtained features are in line with our physical intuition of polarons, the new methodology allows the authors to pinpoint precisely the electronic and vibrational states that contribute to making the polaron. A striking result, which had been missed in previous work, is that, contrary to common belief, polarons in LiF arise not only from the interaction with optical phonons but also from the interaction with piezoacoustic phonons—that are responsible for the piezoelectric effect.
We can expect many more surprises as the method is applied to new and more complex materials. One can envision that the approach could be generalized to include many-body interactions or to tackle excited polaron states. But even in its present version, the new methodology opens up exciting prospects for studying polarons in low-dimensional materials, correlated-electron systems, and topological quantum matter. An all-important application would be studying how polarons transport electrical charge in materials—a problem beyond the reach of previous models. Accurate polaron-transport models would significantly impact the ab initio design of many optoelectronic materials that hold promise for a wide range of applications—not only OLEDs and touch screens but also organic transistors, solar-driven photocatalysts, and hybrid and organic solar cells. A century after Landau’s seminal remarks, we are getting up close and personal with polarons, and this progress might soon be felt in our everyday lives.
This research is published in Physical Review Letters and Physical Review B.
References
- L. Landau, “Uber die Bewegung der Elektronen im Kristallgitter,” Phys. Z. Soviet. 3, 664 (1933).
- W. H. Sio, C. Verdi, S. Poncé, and F. Giustino, “Polarons from first principles, without supercells,” Phys. Rev. Lett. 122, 246403 (2019).
- W. H. Sio, C. Verdi, S. Poncé, and F. Giustino, “Ab initio theory of polarons: Formalism and applications,” Phys. Rev. B 99 (2019).
- D. Emin, Polarons (Cambridge University Press, Cambridge, 2013)[Amazon][WorldCat].
- L. D. Landau and S. I. Pekar, “Effective mass of a polaron,” Zh. Eksp. Teor. Fiz. 18, 419 (1948).
- H. Fröhlich, H. Pelzer, and S. Zienau, “Properties of slow electrons in polar materials,” Philos. Mag. 41, 221 (1950).
- R. P. Feynman, “Slow electrons in a polar crystal,” Phys. Rev. 97, 660 (1955).
- A. Mishchenko, N. Prokof’ev, A. Sakamoto, and B. Svistunov, “Diagrammatic quantum Monte Carlo study of the Fröhlich polaron,” Phys. Rev. B 62, 6317 (2000).
- J. T. Devreese and A. S. Alexandrov, “Fröhlich polaron and bipolaron: Recent developments,” Rep. Prog. Phys. 72, 066501 (2009).
- C. Franchini, G. Kresse, and R. Podloucky, “Polaronic hole trapping in doped BaBiO3,” Phys. Rev. Lett. 102, 256402 (2009).