Neural Networks Take on Open Quantum Systems
Neural networks are behind technologies that are revolutionizing our daily lives, such as face recognition, web searching, and medical diagnosis. These general problem solvers reach their solutions by being adapted or “trained” to capture correlations in real-world data. Having seen the success of neural networks, physicists are asking if the tools might also be useful in areas ranging from high-energy physics to quantum computing [1]. Four research groups now report on using neural network tools to tackle one of the most computationally challenging problems in condensed-matter physics—simulating the behavior of an open many-body quantum system [2–5]. This scenario describes a collection of particles—such as the qubits in a quantum computer—that both interact with each other and exchange energy with their environment. For certain open systems, the new work might allow accurate simulations to be performed with less computer power than existing methods.
In an open quantum system, one typically wants to find the “steady states,” which are states that do not evolve in time. A formal theory for determining such states already exists [6]. The computational difficulty arises when the system contains more than a few quantum particles. Consider a (closed) collection of N spins that can point either up or down. The amplitude of the wave function for a given spin configuration (say, up, down, up, up,…) is a complex number whose absolute value squared gives the probability of observing the configuration. To describe the entire spin system, a complex number has to be specified for each of the 2Npossible states. Simply storing this information for just 20 spins would take about 8 gigabytes of RAM, and the amount would double with each additional spin. Handling the same number of spins in an open system is even harder because the spins must be described by a “density matrix” 𝜌 with 2N×2N matrix elements.
The attraction of a neural network is that it can potentially approximate the wave function, or density matrix, with a lot less information. A neural network is like a mathematical “box” that takes as its input a string of numbers (a vector or tensor) and outputs another string. The box is a parametrized function, and its parameters are optimized for a given task. For the specific case of simulating an N-body quantum system, the neural-network function serves as a “guess” for the wave function, and the states of the N objects serve as inputs. Researchers then optimize the function parameters by having the network “learn” from real or simulated measurement data or by minimizing a physical quantity that depends on the wave function. Once the right guess is in hand, it can be used to calculate other physical properties, and with far fewer than 2N parameters.
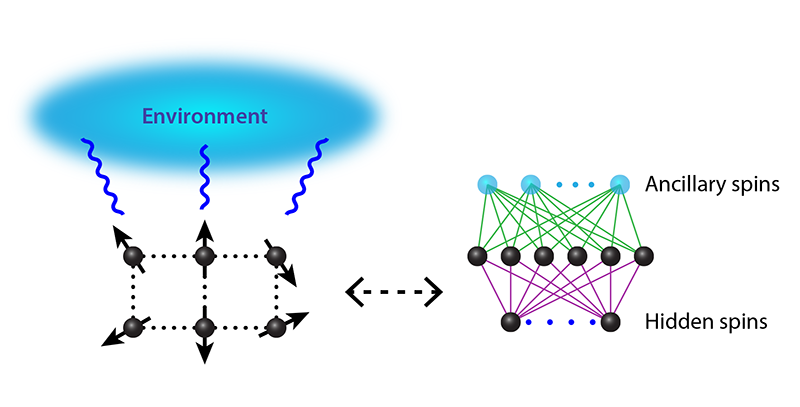
In a 2017 paper, Carleo and Troyer showed that a neural network called a restricted Boltzmann machine [7] could—with a small tweak—be used to represent states of a closed system of many interacting spins [8]. The input for this machine is a string of 0’s and 1’s—mimicking the up or down state of spins in an array—and its output is a complex number that provides the amplitude of the wave function. In effect, the restricted Boltzmann machine replaces the interactions between spins by “mediated” interactions with some “hidden spins” (Fig. 1).
The four groups carry Carleo and Troyer’s approach to open quantum systems [2–5]. The steady states of such systems are described by the Gorini-Kossakowski-Sudarshan-Lindblad (GKSL) equation [8], d𝜌∕dt=L(𝜌) . This equation looks similar to the regular Schrödinger equation, but it solves for the density matrix 𝜌 instead of a wave function, and it involves the operator L, which is effectively the Hamiltonian plus some energy-loss terms.
The GKSL steady states satisfy d𝜌∕dt=0, and to find them, the groups had to address three challenges. First, they had to design a neural network function that represents a density matrix. Second, they needed to define a “cost function.” This function expresses the difference between the neural network and the true quantum state and, when minimized, yields the density matrix corresponding to the desired steady state. Finally, they had to find a way to perform this minimization numerically. Although they all worked independently, the four teams arrived at fairly similar solutions to these problems.
Three of the teams—Hartmann and Carleo [3], Nagy and Savona [4], and Vicentini et al. [5]—followed an idea from a 2018 paper [9] and described the wave function for the quantum system and its environment by adding a set of “ancillary” spins to the restricted Boltzmann machine (Fig. 1). These extra spins ensure that the output of the neural network has the mathematical properties of a density matrix. Yoshioka and Hamazaki, however, derived the density matrix without the ancillary spins and, in turn, relied on a mathematical trick when using the matrix to calculate physical quantities [2].
The groups also varied in how they defined the cost function. Two teams used an indirect approach, based on a so-called Hermitian operator, that has a guaranteed minimization procedure [2, 5]. The two other teams opted for a more direct approach that requires more complex minimization methods [3, 4]. Finally, all of the teams used some form of variational Monte Carlo scheme [9] for the minimization step.
Each group tested their neural network approach by finding the steady states of popular toy models: the dissipative transverse-field Ising model in 1D [2, 5]; the XYZ model in 1D [2] and 2D [4]; and the anisotropic Heisenberg model in 1D [3]. Taking all the results together, the researchers considered system sizes that ranged from 4 to 16 spins. They also compared their steady-state solutions with those found from traditional approaches such as tensor networks and numerical integration, finding striking agreement. For one particular case, Hartmann and Carleo found that a solution required 40 fewer parameters than the tensor network approach [3], an encouraging sign for neural networks.
Practitioners of machine learning are notorious for replacing theoretically motivated, carefully hand-crafted models with a one-size-fits-all model involving optimization techniques that are “blind” to the application. This approach can work embarrassingly well, and there is a good chance that neural networks will become established tools for treating some open quantum systems. Until then, these approaches need to prove their value beyond toy models—as has increasingly been done for the methods of closed quantum systems. For example, can the new approaches handle more spins, longer-range interactions, higher dimensions, the fermion “sign problem,” or quantum particles that are more complex than spins? Another unknown is whether a neural network ansatz can be adapted to specific physical settings, for example when simplifying symmetries in the system or environment are known.
The ultimate toughness test would be to simulate a system whose dynamics retain a memory of the past by virtue of a strong interaction with the environment (non-Markovian dynamics). Capturing the relevant interaction, however, may ultimately require a quantum neural network, which is run by algorithms that are specifically designed for quantum computers.
This research is published in Physical Review Letters and Physical Review B.
References
- G. Carleo et al., “Machine learning and the physical sciences,” arXiv:1903.10563.
- N. Yoshioka and R. Hamazaki, “Constructing neural stationary states for open quantum many-body systems,” Phys. Rev. B 99, 214306 (2019).
- M. J. Hartmann and G. Carleo, “Neural-network approach to dissipative quantum many-body dynamics,” Phys. Rev. Lett. 122, 250502 (2019).
- A. Nagy and V. Savona, “Variational quantum Monte Carlo method with a neural-network ansatz for open quantum systems,” Phys. Rev. Lett. 122, 250501 (2019).
- F. Vicentini, A. Biella, N. Regnault, and C. Ciuti, “Variational neural-network ansatz for steady states in open quantum systems,” Phys. Rev. Lett. 122, 250503 (2019).
- H.-P. Breuer and F. Petruccione, The Theory of Open Quantum Systems (Oxford University Press, Oxford, 2002)[Amazon][WorldCat].
- P. Mehta, M. Bukov, C.-H. Wang, A. G. R. Day, Clint Richardson, C. K. Fisher, and D. J. Schwab, “A high-bias, low-variance introduction to Machine Learning for physicists,” Phys. Rep. 810, 1 (2019).
- G. Carleo and M. Troyer, “Solving the quantum many-body problem with artificial neural networks,” Science 355, 602 (2017).
- F. Becca and S. Sandro, Quantum Monte Carlo approaches for correlated systems, (Cambridge University Press, Cambridge, 2017)[Amazon][WorldCat].