The Brain—as Critical as Possible

Moritz Helias

Viewpoint

The Brain—as Critical as Possible

Moritz Helias

Institute of Neuroscience and Medicine, Jülich Research Centre, Jülich, Germany
Faculty of Physics, RWTH Aachen University, Aachen, Germany

March 1, 2021• Physics 14, 28

A constant bombardment of stimuli drives the brain’s dynamics away from a critical point to a “quasicritical” state.

Figure caption — **Figure 1:** Critical and quasicritical states in neural networks. (Top) Directed percolation in a critical branching model causes avalanche-like activity after initial activation (red dot), with no spontaneous reactivation ( $p_{s} = 0$ ). (Bottom) Spontaneous activations (blue dots, $p_{s} > 0$ ) start avalanches at any time, increasing $T$ and $S$ and thus decreasing the critical exponents $𝜏_{T}$ and $𝜏_{S}$ . This state is known as the quasicritical state.

The dynamics of many diverse physical systems can be described by a single mathematical model. Systems that seem to have little in common—water percolating through sand or cracks propagating through rock, for example—are all critical phenomena in the same “universality class,” (see Common Ground in Avalanche-Like Events). Some investigations have suggested that networks of neurons in the brain represent another critical system in this universality class, while others have revealed neuronal behavior that deviates from criticality. Now, Leandro Fosque, at Indiana University Bloomington, and colleagues show that the brain may be “quasicritical,” driven away from the critical point by the ongoing barrage of external stimuli [1]. They find that this shift is not arbitrary; it occurs in a way that maximizes the brain’s responsiveness to stimuli—a characteristic that is central to how the brain processes information.

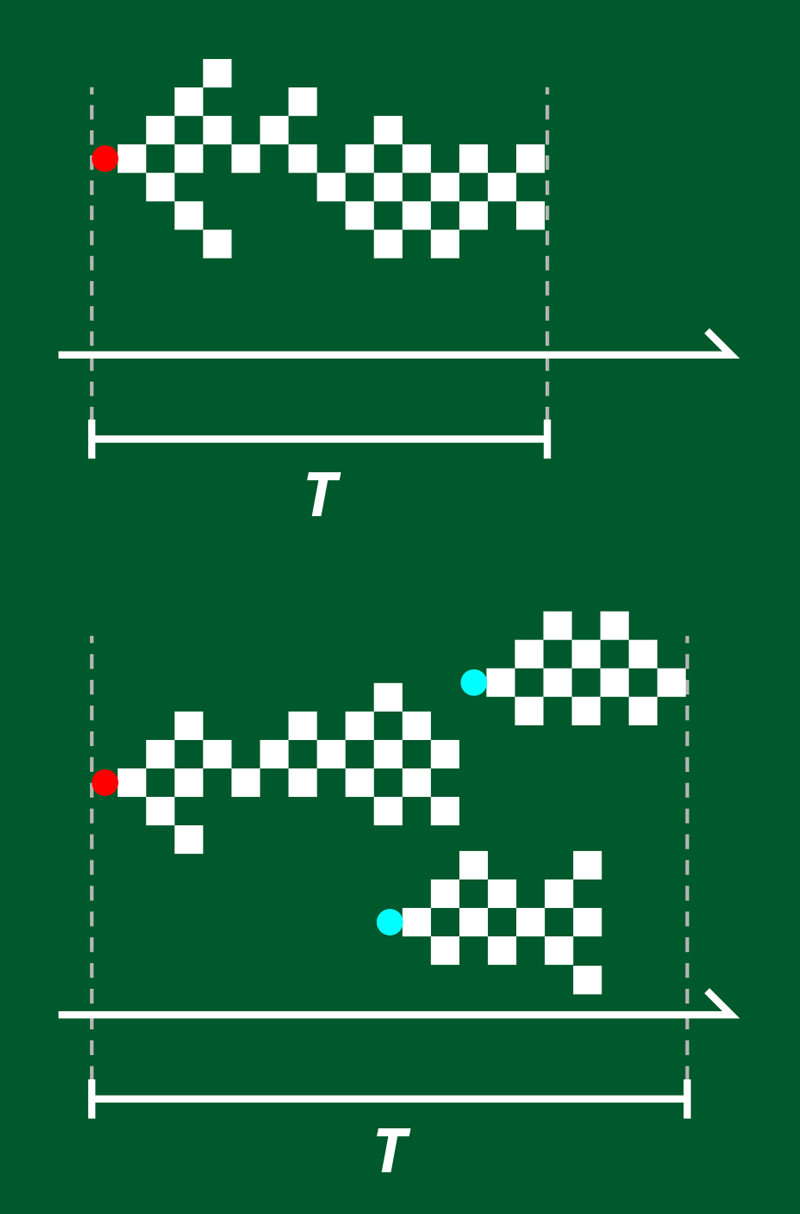
In the brain, criticality refers to the way in which neuronal activity is triggered by a stimulus, such as a sensory input. This activity propagates as a series of avalanches—periods of time $T$ during which $S$ neurons fire in brief succession. Distributions of $T$ and $S$ over time obey power laws, indicative of scale-free, critical behavior [2]. In neural networks cultured in vitro, the corresponding power-law exponents $𝜏_{T}$ and $𝜏_{S}$ (which describe the distribution over time of avalanches with certain $T$ and $S$ values) are constant and are compatible with a universality class that can be modeled by a “directed percolation” branching process (Fig. 1). In this model, each node represents a neuron firing, and the branches represent activity propagating from that neuron to one or more “descendants.” The network’s dynamics are critical when the branching parameter (the number of descendants per active neuron) straddles the boundary between two phases: on one side, the cascade is rapidly damped; on the other, the cascade is self-sustaining.

The lab-grown networks that exhibit this universality class are small and relatively simple. But living brains are complex, and although $T$ and $S$ still show a power-law distribution, experiments reveal that $𝜏_{T}$ and $𝜏_{S}$ differ across species, experimental conditions, time, and stimuli—a finding that fundamentally conflicts with them occupying a single universality class [3].

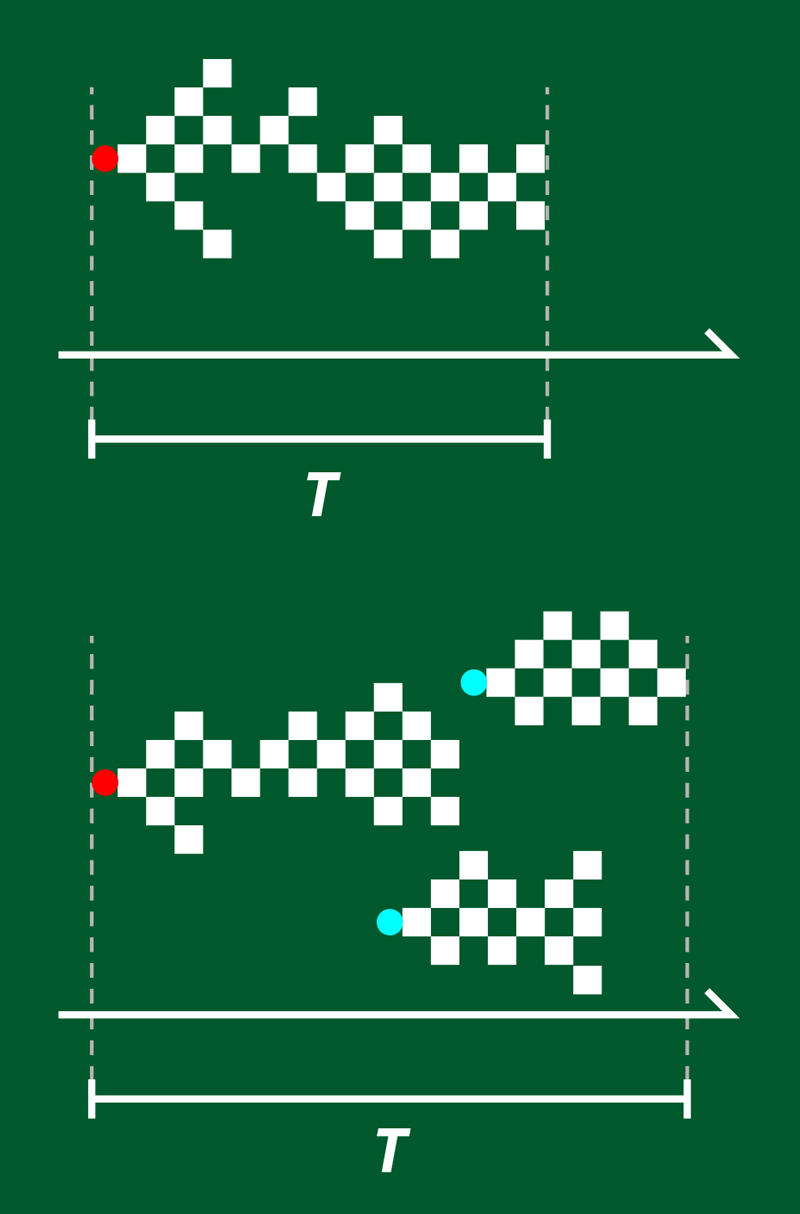
Fosque and colleagues explain the variation in these exponents by combining simulations and an analysis of neuronal data from rodents. Their critical branching model considers an important aspect of directed percolation that differs between neuronal cultures and living brains: the presence of an absorbing state transition. This transition defines the cessation of brain activity that occurs when, by chance, all neurons are inactive at the same instant. Such a state—which is essential for an avalanche to end—is easily reached in a small, isolated network but is harder to achieve in a large, interconnected one.

The reason for this difference is that a cultured network is small, and interactions between neurons are necessarily local. A piece of the in vivo brain’s cortex, in contrast, receives about 50% of its inputs from remote areas [4]. The model by Fosque and colleagues accounts for these remote stimuli by allowing each neuron to be activated spontaneously with a probability $p_{S}$ . In the picture of directed percolation, this means that instead of having just a single neuron ignite an avalanche, avalanches may start spontaneously at any point in time. These intermittent activations increase the duration and size of avalanches and lead to smaller values of $𝜏_{T}$ and $𝜏_{S}$ , meaning that the system is no longer a part of the universality class. This spontaneous activation of avalanches also breaks the strict scale invariance in time, because it implies a characteristic timescale of spontaneous activation $\sim 1 ∕ p_{s}$ , and the system ceases to be critical in a strict sense [5].

Although in living brains the values of $𝜏_{T}$ and $𝜏_{S}$ vary, they do not vary arbitrarily. Rather, as was found recently, $𝜏_{T}$ and $𝜏_{S}$ are tightly linked to one another by a simple linear relation [6] (see New Evidence for Brain Criticality). Fosque and colleagues show that this linear relationship arises when the parameters of their model are tuned to “the point of maximal susceptibility,” meaning that the neurons are most sensitive to stimuli. They call this state “quasicritical”: as critical as possible, given the perturbing, spontaneous activations.

The team’s strong conclusion, that branching models of brain activity can only be truly critical without external drive, has far-reaching consequences. For example, brain regions may operate at different distances from the critical point, depending on their amount of input and—possibly—the function they serve. The picture by Fosque and colleagues also converges with recent findings that the cortex may, in fact, be slightly subcritical [7, 8].

But why should brain dynamics be near to a critical point at all, given that some of the desirable features for a brain—that it is sensitive to external stimuli and that distant regions interact—push the system away from criticality? The answer might be because the critical dynamics of the brain are entangled with its problem-solving abilities. Solvable and unsolvable problems are divided by a sharp boundary, with the hardest-to-solve problems located right at the edge—at a phase transition [9]. An unequivocal confirmation or rejection of this hypothesis would be a major step toward understanding a central principle of biological computation.

The study provokes other interesting questions. For example, how are critical dynamics affected by inhibitory neurons—those that reduce their target’s activity? These cells make up about one-fifth of all cells in the cortex and are crucial for preventing runaway excitation [10]. Another question is, might there be different forms of criticality than that captured by branching models and directed percolation? One possibility that warrants exploring is that the brain might hover between a hyperactive state on one side and an oscillatory instead of a silent state on the other side [6]. Lastly, how do the geometry and density of connections between neurons change critical exponents? Models usually assume random, densely connected networks, leading to mean-field behavior. Could non-mean-field behavior play a role in the brain, possibly leading to different exponents? As research gradually exposes the intriguing link between nonequilibrium statistical physics and brain dynamics, we can look forward to finding answers to these questions and others in the years to come.

References

L. J. Fosque et al., “Evidence for quasicritical brain dynamics,” Phys. Rev. Lett. 126, 098101 (2021).
J. M. Beggs and D. Plenz, “Neuronal avalanches in neocortical circuits,” J. Neurosci. 23, 11167 (2003).
N. Goldenfeld, Lectures on phase transitions and the renormalization group (CRC Press, Boca Raton, 2019)[Amazon][WorldCat].
V. Braitenberg and A. Schüz, Anatomy of the cortex: Statistics and geometry (Springer-Verlag, Berlin, 1991)[Amazon][WorldCat].
R. V. Williams-García et al., “Quasicritical brain dynamics on a nonequilibrium Widom line,” Phys. Rev. E 90, 062714 (2014).
A. J. Fontenele et al., “Criticality between cortical states,” Phys. Rev. Lett. 122, 208101 (2019).
V. Priesemann et al., “Spike avalanches in vivo suggest a driven, slightly subcritical brain state,” Front. Syst. Neurosci. 24 (2014).
J. Wilting and V. Priesemann, “Between perfectly critical and fully irregular: A reverberating model captures and predicts cortical spike propagation,” Cereb. Cortex 29, 2759 (2019).
P. Cheeseman et al., “Where the really hard problems are,” in Proceedings of the 12th International Joint Conference on Artificial Intelligence, IJCAI’91, Vol. 1 (Morgan Kaufmann Publishers Inc., San Francisco, 1991), p. 331[Amazon][WorldCat].
C. van Vreeswijk and H. Sompolinsky, “Chaos in neuronal networks with balanced excitatory and inhibitory activity,” Science 274, 1724 (1996).

About the Author

Moritz Helias is a group leader at the Jülich Research Centre, Germany, and an assistant professor in physics at the RWTH Aachen University, Germany. His research interests are in recurrent biological networks and neuronal information processing, and the development of statistical physics and field theory approaches applied to these domains.