Imaginary Magnetic Fields in the Real World

Nerses Ananikian; Ralph Kenna

Viewpoint

Imaginary Magnetic Fields in the Real World

Nerses Ananikian

A. I. Alikhanyan National Science Laboratory, 0036 Yerevan, Armenia

Ralph Kenna

Applied Mathematics Research Centre, Coventry University, Coventry CV1 5FB, United Kingdom

January 5, 2015• Physics 8, 2

Imaginary magnetic fields predicted by the fundamental theory of phase transitions can be realized experimentally.

Figure caption — **Figure 1:** How Lee-Yang zeros signal a phase transition. In an ordering magnet, the critical point $T_{c}$ is marked by a divergence in the magnet’s susceptibility $χ$ . Above $T_{c}$ , the Lee-Yang zeros, which lie on the unit circle in the complex $z = exp (- H / k T)$ plane, lie away from the physically meaningful positive $z$ axis. At $T_{c}$ , the zeros pinch the real axis.

Ferromagnetic materials like cobalt and iron produce magnetic fields whose magnitudes are measured by real numbers. Imaginary or complex fields are, however, essential in the fundamental theory that underlies the statistical physics of phase transitions, such as those associated with the onset of magnetization. Long thought to be merely mathematical constructs, a realization of these imaginary fields has now been observed in magnetic resonance experiments performed on the spins of a molecule [1]. Following an earlier theoretical proposal, Xinhua Peng at the University of Science and Technology of China and her colleagues have shown that imaginary magnetic fields associated with a spin bath—in this case, the molecule—approaching a phase transition can be related to the quantum coherence of a probe spin coupled to the bath [1]. The demonstration that this connection exists in a physical system is important at a fundamental level, and could lead to new ways of studying phase transitions in complex, many-bodied materials.

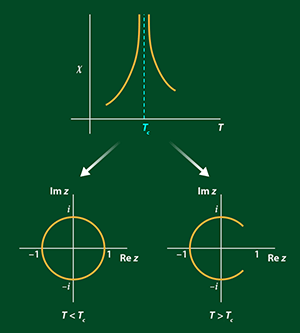
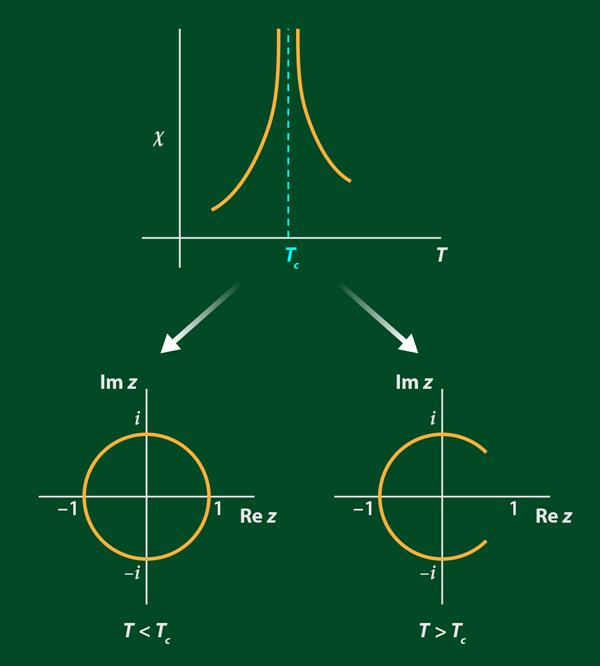
One of the simplest systems to exhibit a continuous (second-order) phase transition is the ferromagnetic Ising model. In this system, which can describe magnets, binary alloys and lattice gasses, atomic spins arranged on a lattice can be in one of two discrete states—up or down. Interactions between neighboring spins favor their collective alignment into a magnetic state below a critical temperature $T_{c}$ . Above this temperature, the spins tend to be randomly oriented and the system lacks a spontaneous magnetization. The response of the spins to changes in external parameters, such as the magnetic field or temperature, is given by functions such as the susceptibility. At the critical point, $T_{c}$ , of an idealized system of infinite size (the so-called thermodynamic limit), the susceptibility and certain other response functions diverge.

In 1952, C. N. Yang and T. D. Lee developed a fundamental theory that relates the phase transition in the Ising model and other systems to the mathematical form of their partition functions [2]. This function, which involves thermal energies distributed across all possible microscopic states, can be written as a polynomial function of the variable $z = exp (- H / k T)$ , where $H$ is a magnetic field, $T$ is the temperature and $k$ is Boltzmann’s constant. The fundamental theorem of algebra says that a polynomial of degree $n$ has $n$ roots. If the coefficients of such a polynomial are real and positive, its roots are complex or negative. For many finite-sized statistical mechanical systems, the partition function is such a polynomial and has complex-valued roots.

Lee and Yang proved that, under quite general conditions, the roots of the partition function for the ferromagnetic Ising model lie on the unit circle in the complex $z$ plane (or on the imaginary axis of the complex magnetic-field plane) (Fig. 1). These roots, called Lee-Yang zeros, lie away from the physically meaningful positive $z$ axis if the temperature is greater than $T_{c}$ . As the temperature is lowered, the roots move down and begin to pinch the real axis, closing in completely when the critical point is reached in the thermodynamic limit.

Lee-Yang theory is a powerful concept in statistical physics: Besides their fundamental importance, the distributions of the Lee-Yang zeros can deliver unambiguous signs of a phase transition and its properties, in circumstances where corresponding signals in thermodynamic functions (such as susceptibility) might be more difficult to discern. For example, the density of Lee-Yang zeros takes on a nonzero value when a spontaneous magnetization is present below $T_{c}$ . But until now, these partition function zeros, which occur at complex values of the magnetic field, were thought be unphysical with no real manifestation in the physical world. The work of Peng et al., however, shows that they can be accessed experimentally.

Their experiments are based on a theoretical proposal by two of the authors, Ren-Bao Liu and Bo-Bo Wei [3]. They considered a “bath” of Ising spins and showed, theoretically, that the partition function of the bath under a complex magnetic field is equivalent to the quantum coherence of a probe spin coupled to the spin bath. (Quantum spin coherence is a measure of the extent to which a spin holds its orientation as time evolves.) Liu and Wei found that the times at which the quantum coherence reaches zero are equivalent to the complex fields at which the partition function vanishes—that is, the fields that produce the Lee-Yang zeros.

To simulate a coupled probe-bath system, the researchers used a liquid of trimethylphosphite (TMP) molecules. TMP has nine hydrogen atoms and one phosphorous atom, each with its own spin. The nine hydrogen spins thus play the role of the spin bath and the phosphorous functions as the probe spin. Peng et al. first prepared the probe spin in a quantum superposition between up and down and then used liquid-state nuclear magnetic resonance (NMR) to determine the times at which the spin’s coherence dropped to zero. These zeros in the coherence correspond directly to the Lee-Yang zeros, which were then used to reconstruct the free energy and partition function of the spin bath. Although the system is small, the critical temperature is estimated as that which leads to a nonzero density of Lee-Yang coherence zeros.

This is the first direct observation of imaginary-field, Lee-Yang zeros in real experiments and, as such, is an important realization of a hitherto theoretical, and supposedly unphysical, notion in statistical physics. The experiments also confirm a profound connection between a static entity (the complex magnetic field in thermodynamics) and dynamical properties of quantum systems (coherence). This research demonstrates how a quantum coherence probe can be used to study thermodynamics in the complex plane in finite systems, which is important in statistical physics at a fundamental level. While this experiment focuses on complex zeros of the Lee-Yang type (i.e., in a complex external magnetic field) in a ferromagnetic system, one could imagine also looking for such Lee-Yang zeros in antiferromagnetic systems, or for their temperature counterparts (Fisher zeros [4]). Peng et al.’s approach could also help in the study of complicated real-life systems in which the zeros can’t easily be calculated or require experimental verification. It might reveal new quantum phenomena that would otherwise remain hidden if one were to restrict one’s attention to real, physical parameters.

This research is published in Physical Review Letters.

References

Xinhua Peng, Hui Zhou, Bo-Bo Wei, Jiangyu Cui, Jiangfeng Du, and Ren-Bao Liu, “Experimental Observation of Lee-Yang Zeros,” Phys. Rev. Lett. 114, 010601 (2015)
C. N. Yang and T. D. Lee, “Statistical Theory of Equations of State and Phase Transitions. I. Theory of Condensation,” Phys. Rev. 87, 404 (1952); T. D. Lee and C. N. Yang, “Statistical Theory of Equations of State and Phase Transitions. II. Lattice Gas and Ising Model,” 87, 410 (1952)
B.-B. Wei and R.-B. Liu, “Lee-Yang Zeros and Critical Times in Decoherence of a Probe Spin Coupled to a Bath,” Phys. Rev. Lett. 109, 185701 (2012)
M. E. Fisher in Statistical Physics and Solid State Physics, Lectures in Theoretical Physics, edited by W. E. Brittin (University of Colorado Press, Boulder, 1965)

About the Authors

Nerses Ananikian is a Professor at A. I. Alikhanyan National Science Laboratory in Yerevan, Armenia. He obtained his Ph.D. from Yerevan Physics Institute in 1983. His group works on the fundamental physics of thermal entanglement, partition function zeros and dynamic systems. He has been a visiting scientist at Dublin Institute for Advanced Studies in Ireland; Bonn University; ICTP in Trieste; Hong Kong Buptist University; CEA Saclay in France; Universita’ degliStudidell’Insubria in Italy; Universidade Federal de Lavras in Brazil; and Coventry University’s Applied Mathematics Research Centre in UK.

Ralph Kenna is a Professor at Coventry University’s Applied Mathematics Research Centre (AMRC) in England. He obtained his Ph.D. from the Karl-Franzens Universität, Graz, Austria in 1993 and, after posts in the University of Liverpool and Trinity College Dublin he settled in Coventry where he established one of the UK’s largest statistical physics groups as part of the AMRC. He has worked extensively on phase transitions and critical phenomena but also has interests in applications of statistical physics to sociology and humanities. He has been a visiting scientist at Universität Leipzig, Germany, Université de Lorraine, France and the Institute of Condensed Matter Physics in Lviv, Ukraine.