Topological Phases
The 2016 Nobel Prize in Physics was awarded to David Thouless, Duncan Haldane, and Michael Kosterlitz “for theoretical discoveries of topological phase transitions and topological phases of matter” (see 7 October 2016 Focus story). The trio began researching these problems in the late 1970s and early 1980s. But as this collection of articles from the Physics archive demonstrates, 30 to 40 years later, their discoveries are still influencing research across a broad range of fields, from condensed matter, to ultracold atoms, to photonics.
Phase Transitions in a 2D World
In the 1970s, Kosterlitz and Thouless recognized the role of topological defects (vortices) in allowing phase transitions in two-dimensional systems. Their theories have been applied to thin films of superfluid helium, thin-film superconductors and a variety of other systems. As Pierbiagio Pieri describes in a Viewpoint from 2015, atomic physicists observed a Kosterlitz-Thouless transition (also known as a Berezinskii-Kosterlitz-Thouless transition) in trapped fermions for the first time by analyzing the correlations between ultracold lithium atoms confined to a flat geometry.
No Magnetic Field Required
The 1980 demonstration of the quantum Hall effect (see 15 May 2015 Focus story) marked the discovery of topological quantum matter. The early theory for the phenomenon, in which electrons confined to two dimensions acquire a quantized conductance in the presence of a perpendicular magnetic field, assumed the charges move in a uniform sheet. In 1982, Thouless extended the theory to account for a crystalline lattice, revealing the topological origin of the effect. His work, with key insights from Haldane, led to the realization that the quantum Hall effect can occur without a field in certain materials. This quantum “anomalous” Hall effect has since been observed in several materials, one of which is a thin film of a magnetic topological insulator, as explained in a 2015 Viewpoint by Ke He.

Fractionalized Excitations
Many topological states are characterized by fractionalized excitations, which cannot be associated with a single entity, like an electron or spin, and are a manifestation of collective order. Perhaps the best example is the fractional quantum Hall effect (see 16 October 1998 Focus story) discovered in 1982. Viewpoints by Jainendra Jain and by Kirill Shtengel, both in 2010, describe attempts to understand a fractional quantum Hall effect state that isn’t like the others and that many think may provide the basis for fault-tolerant quantum computing. And in a 2011 Viewpoint, Rahul Roy and Shivaji Sondhi describe a trio of papers predicting that the fractional quantum Hall effect might, like the simpler quantum Hall effect, also occur in some materials without an external magnetic field.

Weird Surface States
In 1983, Haldane developed a theory for certain spin chains that predicted an energy gap, initiating the realization that they have a symmetry-protected topological character. In 2008, researchers discovered 3D topological insulators—insulators with metallic surface states that, just like the Haldane chains, are symmetry protected. As Shou-cheng Zhang describes in a Viewpoint, the same year saw some of the first detailed calculations to predict the electronic structure of such states. And two years later, experiments paved the way to seeing the quantum Hall effect in these states by showing that they can exhibit Landau levels, as explained in a Viewpoint by Jacob Linder.
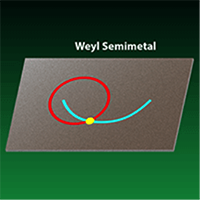
Majorana Modes and Weyl States
Majorana modes and Weyl states are some of the latest examples of states with topological character. Majorana modes can be regarded as fractionalized quantum bits, and Weyl states are excitations that behave analogously to massless fermions. In a Viewpoint, Taylor Hughes describes a 2011 theoretical proposal suggesting that Majorana modes could be found in superconducting topological insulators. In another Viewpoint, Ashvin Vishwanath describes the 2015 discovery of Weyl states in a semimetal and in a photonic crystal.

Topologically Speaking
In a Q&A article, Taylor Hughes explains what he finds fascinating about topological materials, and ponders what their “killer app” might one day be.

Topological Phases with Cold Atoms
Several Viewpoints have highlighted efforts to simulate topological phases with ultracold atoms. In 2011, Ian Spielman reviewed an idea for generating large effective magnetic fields for atoms in an optical lattice—analogous to the fields that drive the quantum Hall effect for electrons. In the same year, Erich Mueller described the experimental demonstration of just such fields. And in 2012, Mueller explained the first experiments to simulate spin-orbit coupling in ultracold Fermi gases, which set the stage for creating certain topological phases with atoms.
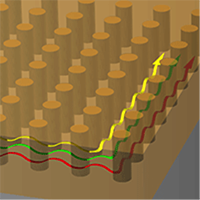
Topology in Photonics
Topological states have also been explored in photonic settings. In a Viewpoint from 2010, Andrew Greentree and Andrew Martin described an idea for designing photonic circuits in which time-reversal symmetry is broken—a step that would allow photons to emulate the integer and fractional quantum Hall effects. And as Mikael Rechtsman explains in his 2015 Viewpoint, a photonic crystal made of garnet rods and copper plates exhibits multiple topologically protected routes for microwaves.
Several Physical Review articles related to the Nobel-prize winners’ research are free to read. The list is available here.


